Chapter 7 Parallel sorting
7.1 Parallel merging
innovation("lean-parallel-merging","T","lean parallel merging")
innovation("PKnuthsort","E","parallel Knuthsort")
dependency("PKnuthsort","Knuthsort")
dependency("PKnuthsort","lean-parallel-merging")The greeNsort® test-bed uses the POSIX pthread library. The APIs of the parallel sorting algorithms require specification of the number of allowed threads as a parameter. This number is split down the recursion tree. The first step to parallelizing a Mergesort is running the recursive branches in parallel.
Figure 7.1: Number of threads per node in parallel splitting
But that is not enough: with parallel branching the maximum parallelism is only achieved at the leaves of the tree (4 in the example). Serial merging prevents proper utilization of cores near the root of the tree. Merging can also be parallelized: by recursively searching for the median in the two sorted sequences to be merged (Cormen et al. (2009)20):
Figure 7.2: Number of threads per node in parallel splitting and parallel merging using recursive medians
This is still not optimal, because the parallelism of the merges is assumed to be a power of two. If there are 6 cores available, this implies that either only 4 are used or that 8 threads are used that compete for 6 cores. This implies context-switching and competing access into the cache-hierarchy. For the sake of robustness greeNsort® prefers to not make the assumption that using more threads than requested is harmless and strives for a parallel merge that will use exactly the requested number of cores by splitting into the appropriate number of percentiles.
Figure 7.3: Number of threads per node in parallel splitting and parallel merging using percentiles
The theoretically most efficient solution is a recursive search procedure that operates not only on the two input vectors but also on a vector of requested percentiles. However, this requires extra dynamically allocated memory structures and and a certain implementation complexity. A much simpler and distance-friendly solution is to loop over the requested percentiles and search in turn for the next percentile in the remaining range. I call this lean-parallel-merging.
7.1.1 Parallel Knuthsort
Using lean-parallel-merging method, the reference algorithm Knuthsort has been parallelized into PKnuthsort and it scales reasonably with the number of available threads. With a single sorting process and 4 threads on the 4-core machine RUNtime goes down to 0.3 (theoretical optimum 0.25). Note this is RUNtime, not CPUtime, hence for 8 processes runTime must double (unlike CPUtime or Energy).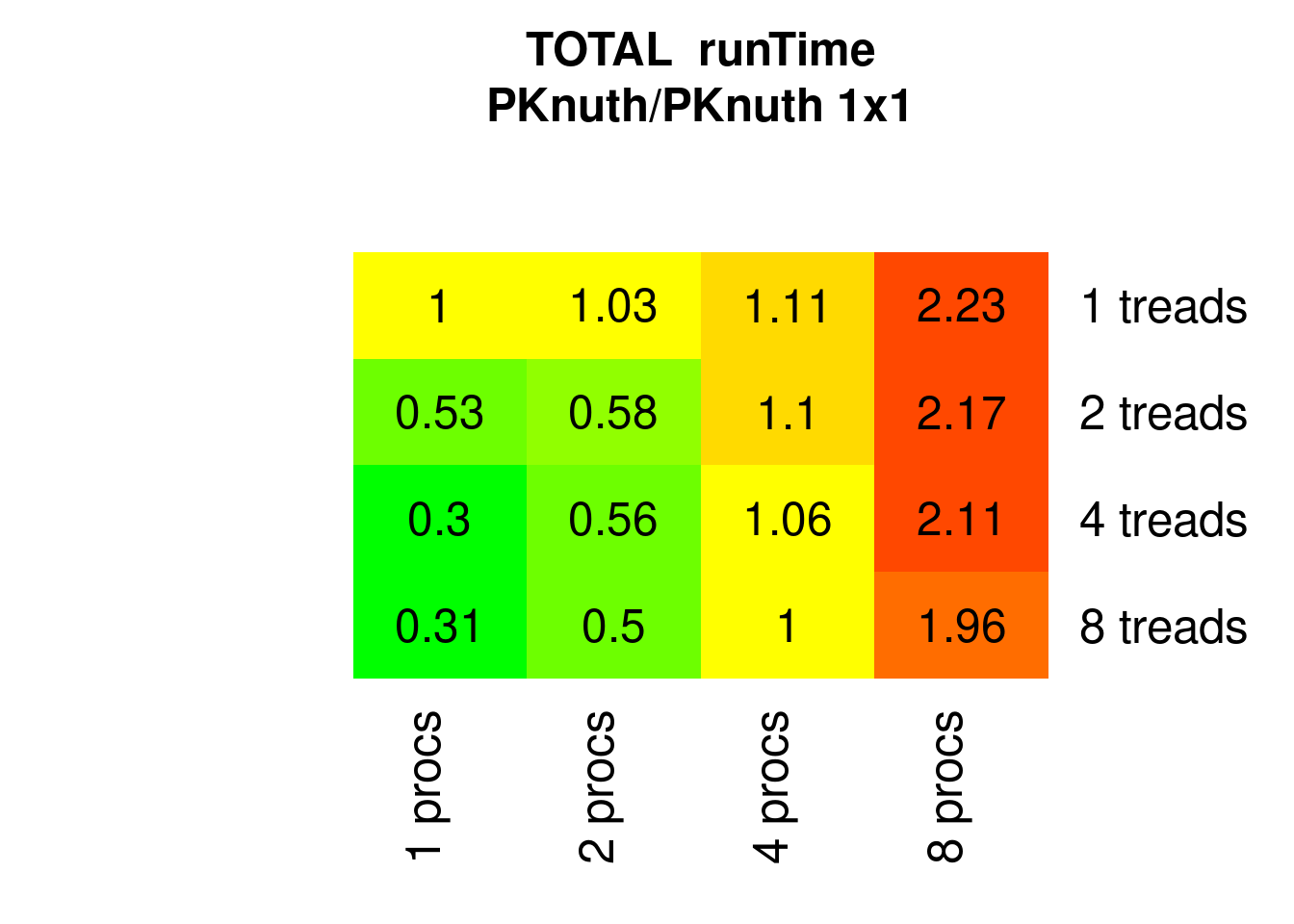
Figure 7.4: Parallel PKnuthsort runTimes relative to 1x1 (1 process 1 thread)
Energy savings by multi-threading are less impressive:

Figure 7.5: Parallel PKnuthsort pcdEnergy relative to 1x1 (1 process 1 thread)
7.1.2 Parallel Frogsorts
innovation("parallel-Symmetric-merging","B","iterative parallel merging")
dependency("parallel-Symmetric-merging","lean-parallel-merging")
innovation("PFrogsort0","E","Parallel Frogsort0")
innovation("PFrogsort1","E","Parallel Frogsort1")
innovation("PFrogsort2","E","Parallel Frogsort2")
innovation("PFrogsort3","E","Parallel Frogsort3")
dependency("PFrogsort0","parallel-Symmetric-merging")
dependency("PFrogsort0","Frogsort0")
dependency("PFrogsort1","parallel-Symmetric-merging")
dependency("PFrogsort1","Frogsort1")
dependency("PFrogsort2","parallel-Symmetric-merging")
dependency("PFrogsort2","Frogsort2")
dependency("PFrogsort3","parallel-Symmetric-merging")
dependency("PFrogsort3","Frogsort3")Here I disclose how to parallelize Frogsort. Like with Knuthsort parallelizing the branches is trivial, except for some care to split the available threads proportional to the imbalanced branch-sizes in Frogsort2 and Frogsort3. Parallelizing the Symmetric-merging is more tricky: it is not possible to parallelize the symmetric-merge at once, because part of the target memory is still occupied with the source data. Hence the parallel merging needs to be done iteratively for the amount of free buffer available. For the balanced Frogsort0 and Frogsort1 under random data this leads to merging 50% of the data, then 25% of the data, and so on. This carries a little more overhead and reduces the parallelism in the final iterations if one considers a minimum number of elements per thread. Still this scales quite well. I call this parallel-Symmetric-merging
Finally, a difference to Knuthsort is the parallelization of the setup phase. Frogsort0 uses a simple loop to setup its triplets, parallelizing is more successful than parallelizing the recursive setup of Frogsort1, Frogsort2, Frogsort3.
In the following Frogsort Scaling section parallel scenarios are compared to serial (1x1). In the following sections Frogsort Speed, Frogsort Energy and Frogsort Footprint each of the 16 scenarios is compared to PKnuthsort.
7.1.2.1 Frogsort Scaling
PFrogsort0 shows multi-threading behavior as good as PKnuthsort (and a little worse when running multiple processes with multiple threads):
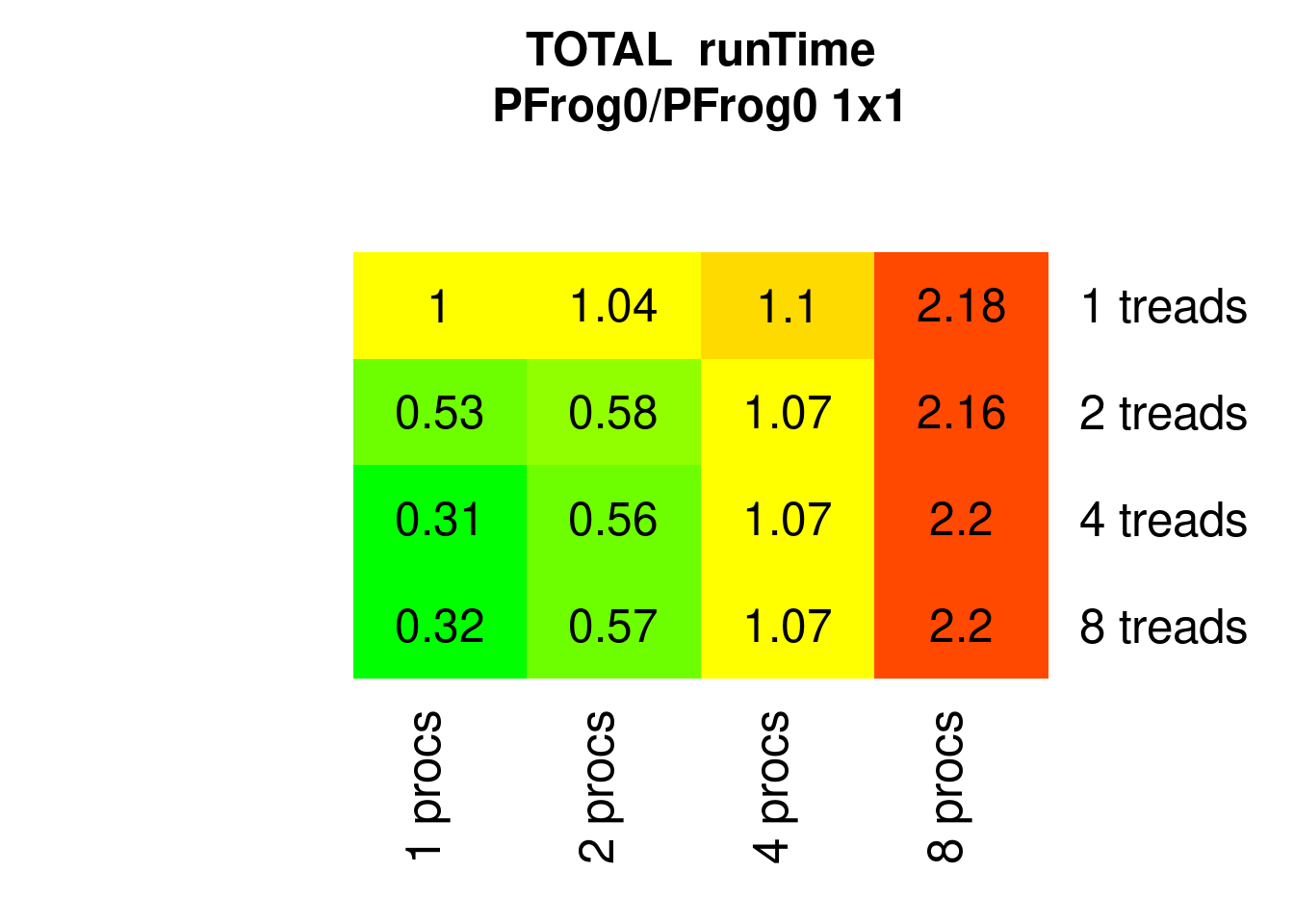
Figure 7.6: Parallel PFrogsort0 runTimes relative to 1x1 (1 process 1 thread)
PFrogsort1 multi-threading behavior is a bit worse (in one process) and a bit better when combined with multiple processes:
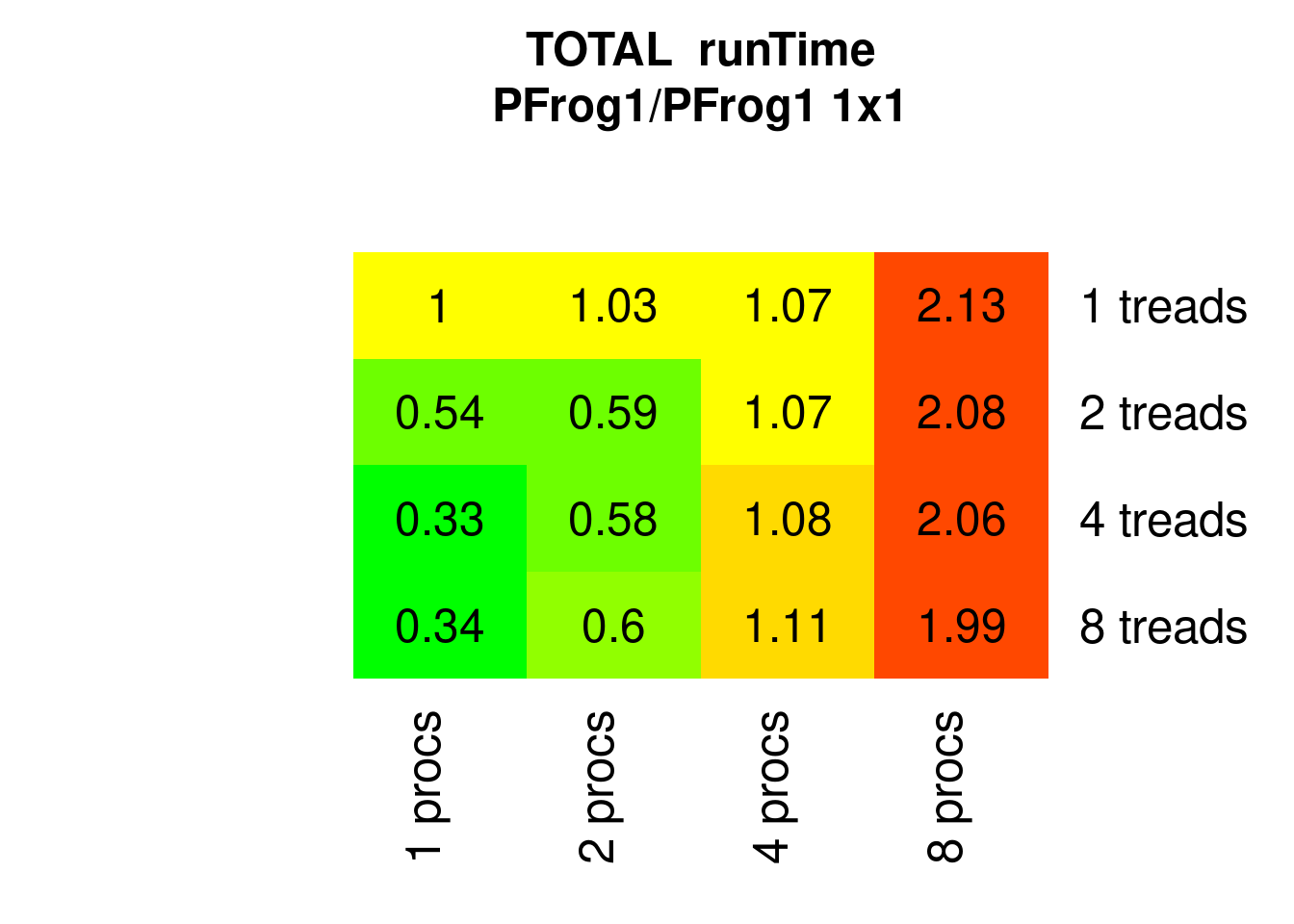
Figure 7.7: Parallel Frogsort1 runTimes relative to 1x1 (1 process 1 thread)
PFrogsort2 does not scale as good, but don’t misinterpret this: the big advantage in serial executions diminishes when running PFrogsort2 in parallel, but can still win over PKnuthsort (see the following sections):
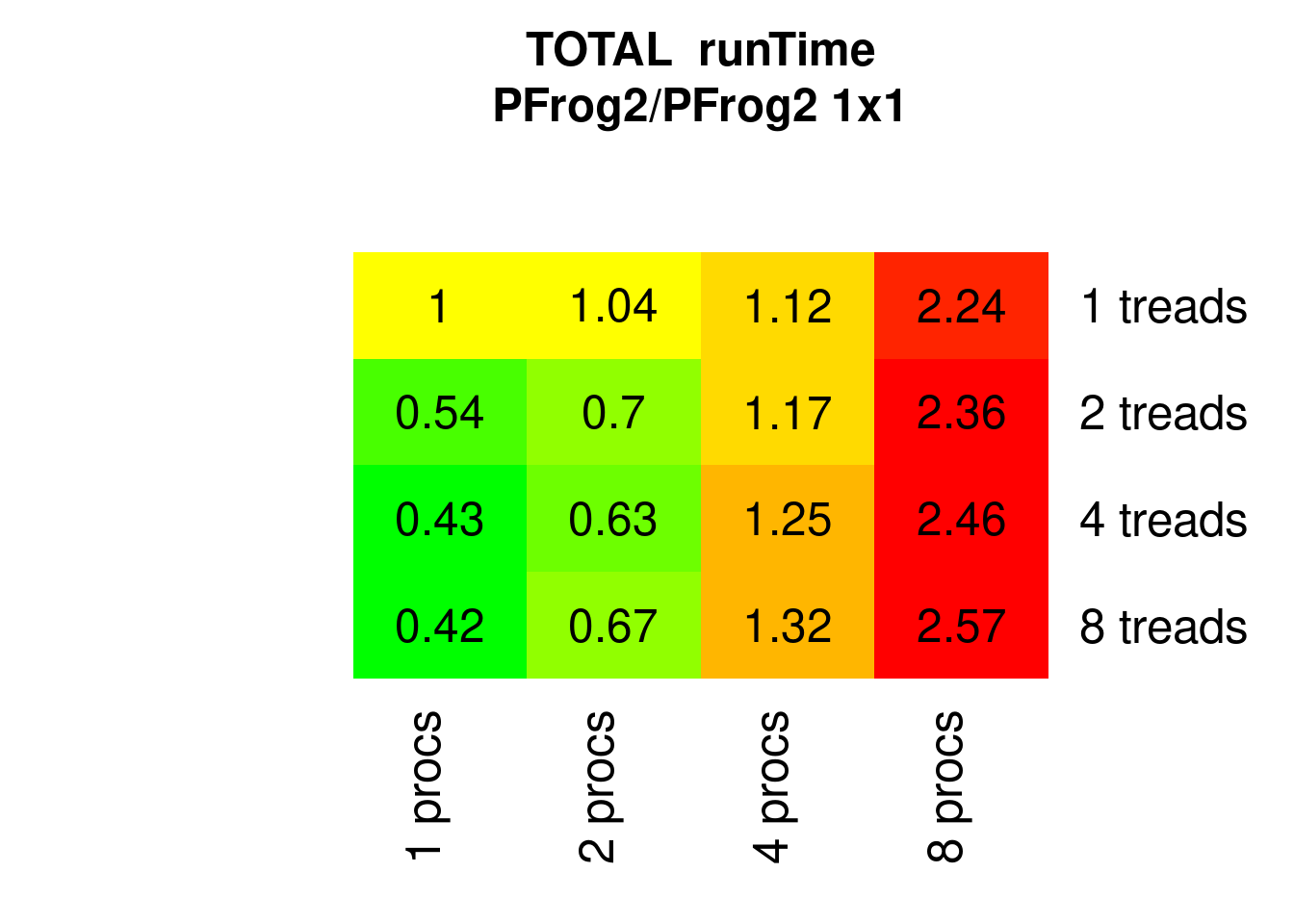
Figure 7.8: Parallel Frogsort1 runTimes relative to 1x1 (1 process 1 thread)
PFrogsort3 gives a similar picture:
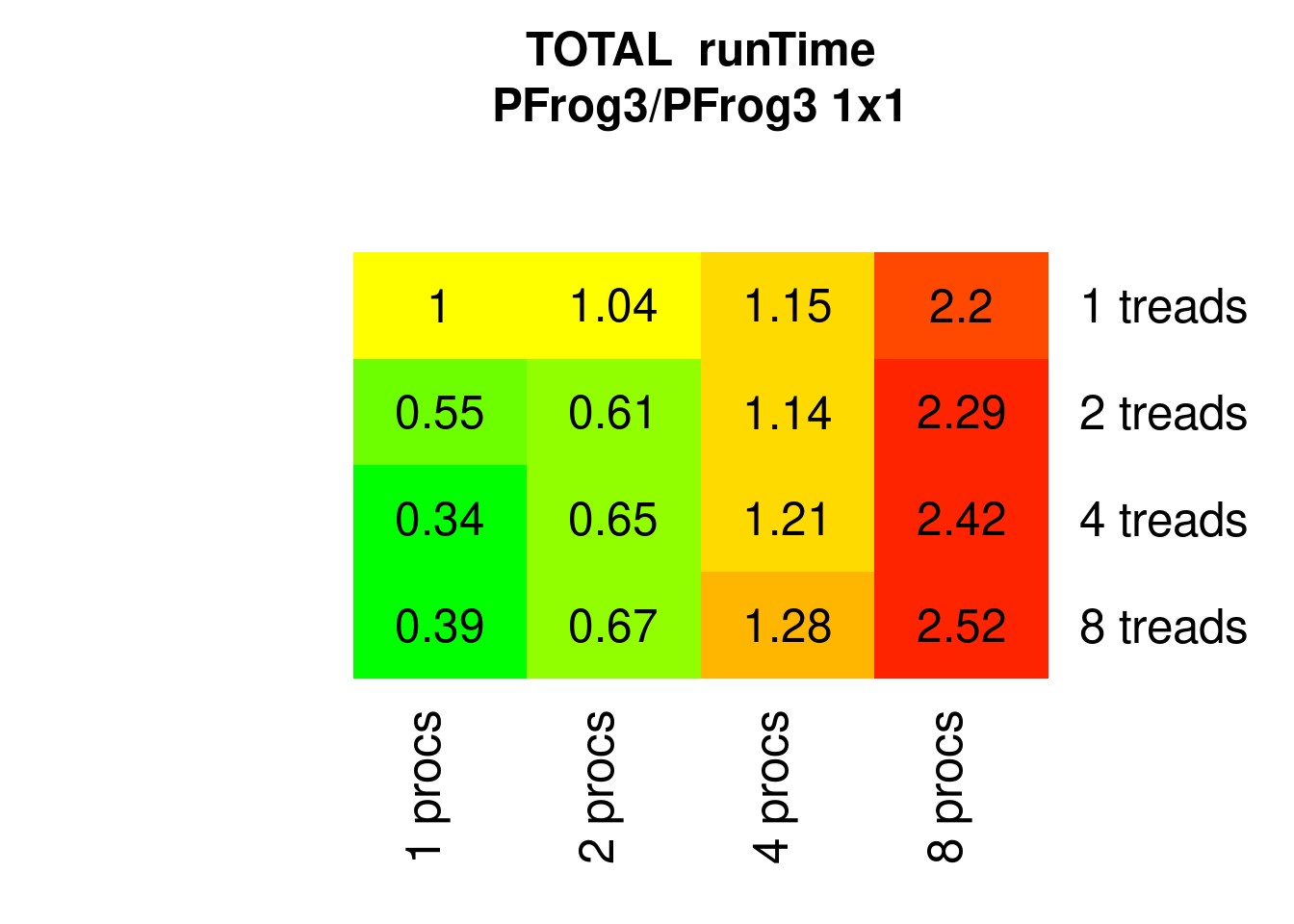
Figure 7.9: Parallel Frogsort1 runTimes relative to 1x1 (1 process 1 thread)
7.1.2.2 Frogsort Speed
PFrogsort0 is consistently faster than PKnuthsort if the number of threads does not exceed the number of physical cores:
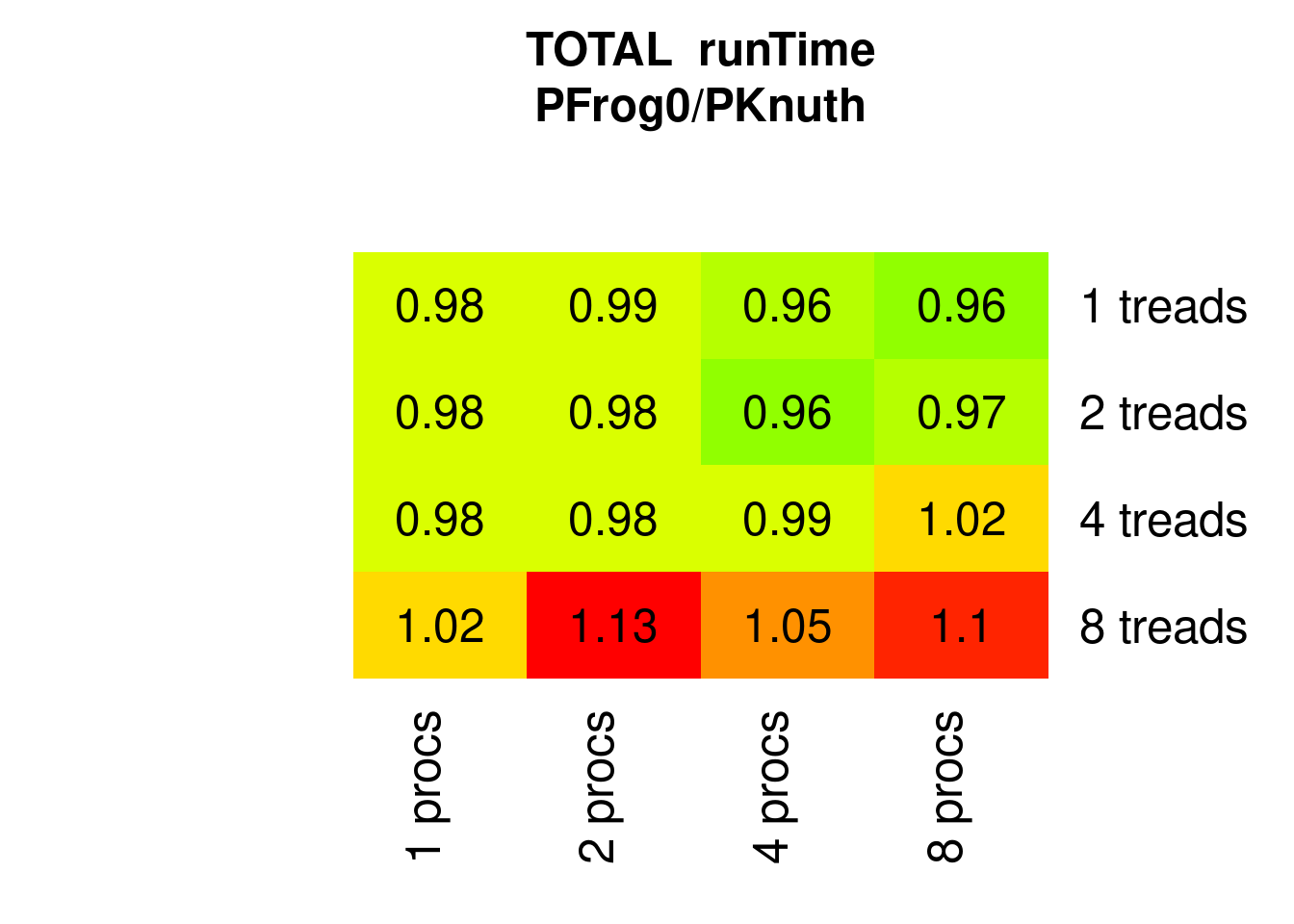
Figure 7.10: Parallel PFrogsort0 speed relative to Knuthsort
PFrogsort1 is somewhat slower than PKnuthsort particularly when multithreaded and without competing processes:
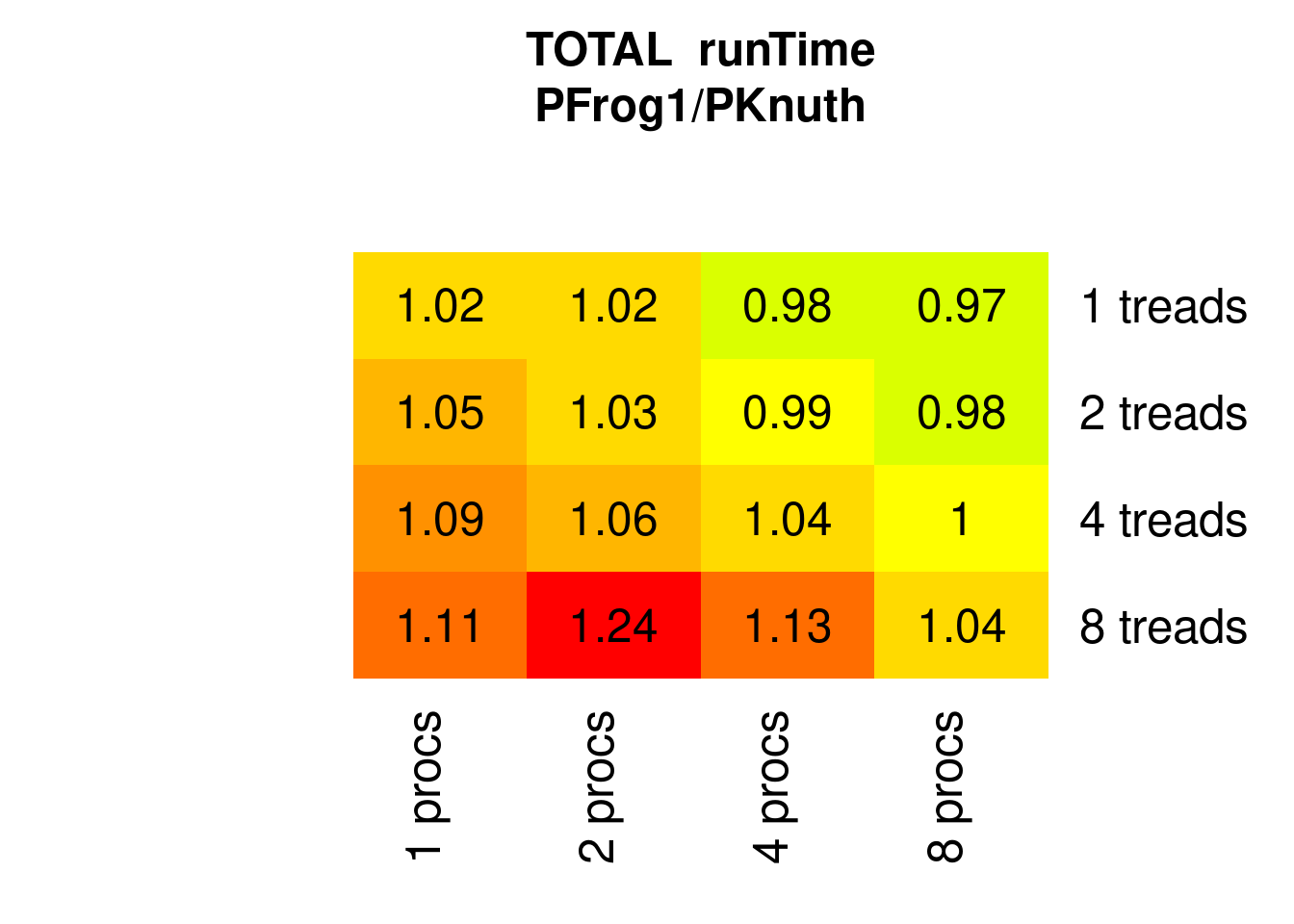
Figure 7.11: Parallel PFrogsort1 speed relative to Knuthsort
PFrogsort2 is faster than PKnuthsort except for high multi-threading and low parallel processes:

Figure 7.12: Parallel PFrogsort2 speed relative to Knuthsort
As a tribute to the low memory-requirement, PFrogsort3 is consistently slower than PKnuthsort:
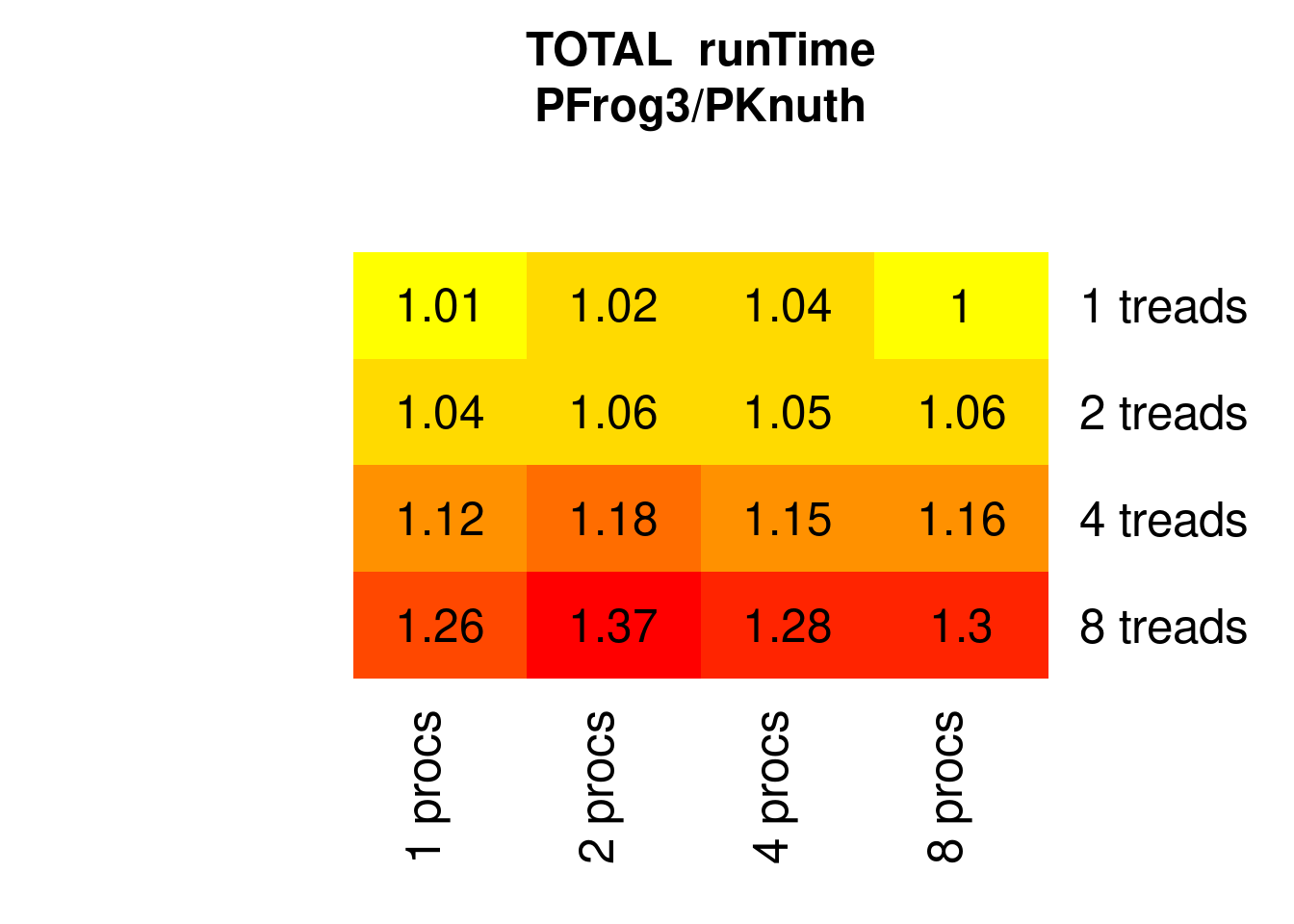
Figure 7.13: Parallel PFrogsort3 speed relative to Knuthsort
7.1.2.3 Frogsort Energy
PFrogsort0 is consistently more energy-efficient than PKnuthsort if the number of threads does not exceed the number of physical cores:
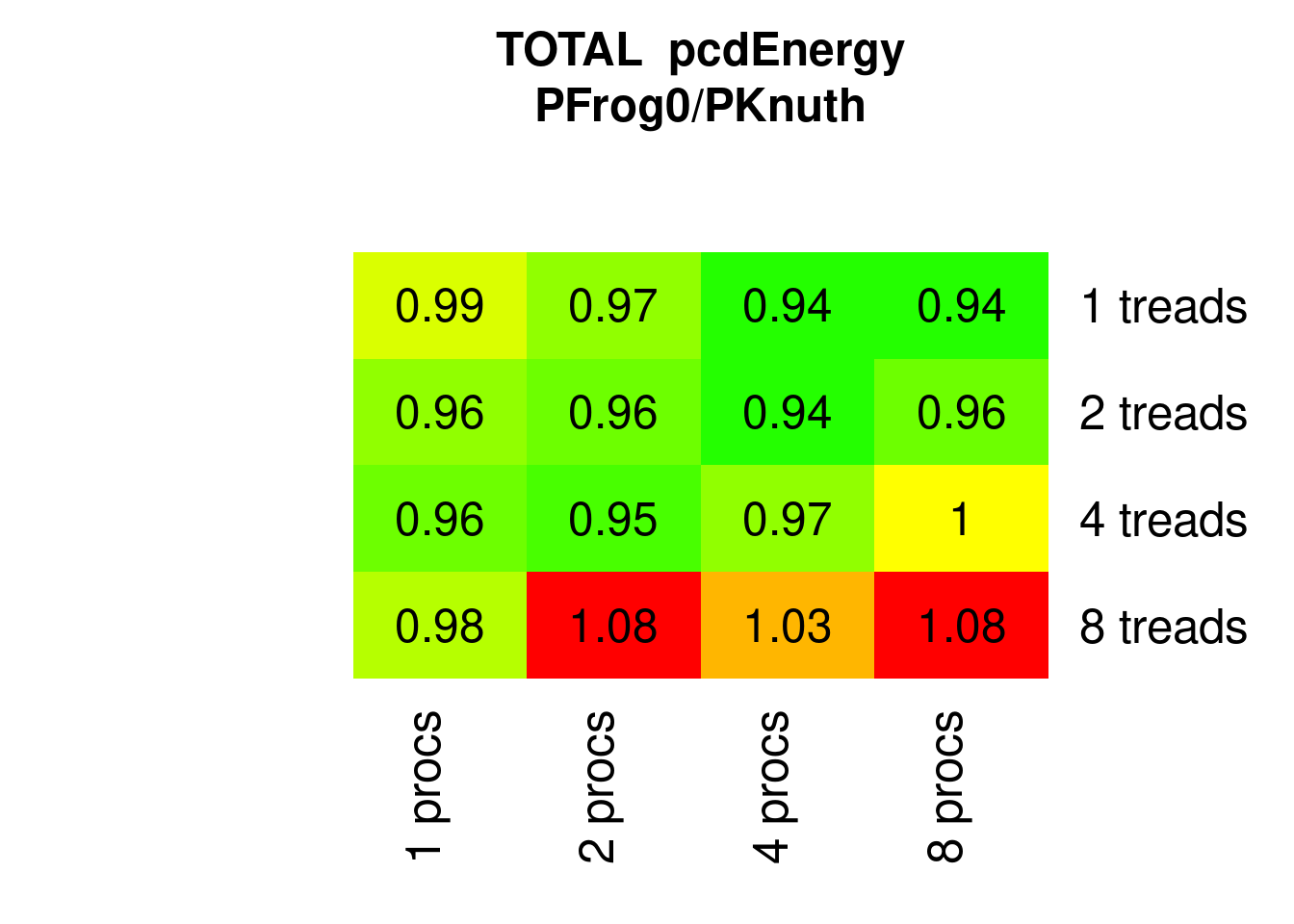
Figure 7.14: Parallel PFrogsort0 Energy relative to Knuthsort
PFrogsort1 needs the same amount of Energy than PKnuthsort – with less %RAM requirements – if the number of threads does not exceed the number of physical cores:
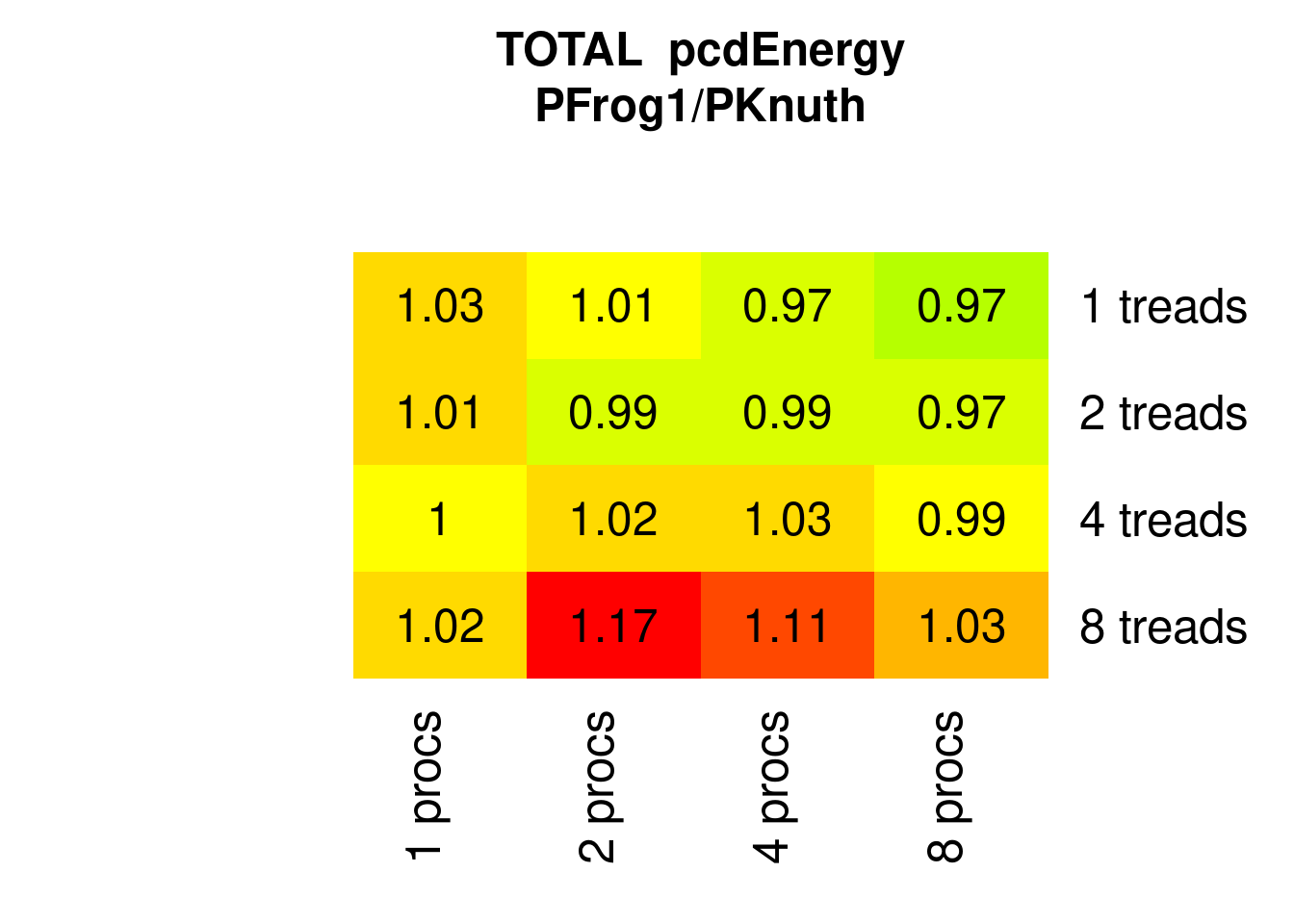
Figure 7.15: Parallel PFrogsort1 Energy relative to Knuthsort
With less memory requirements PFrogsort2 is consistently more energy-efficient than PKnuthsort – if the number of threads does not exceed the number of physical cores:
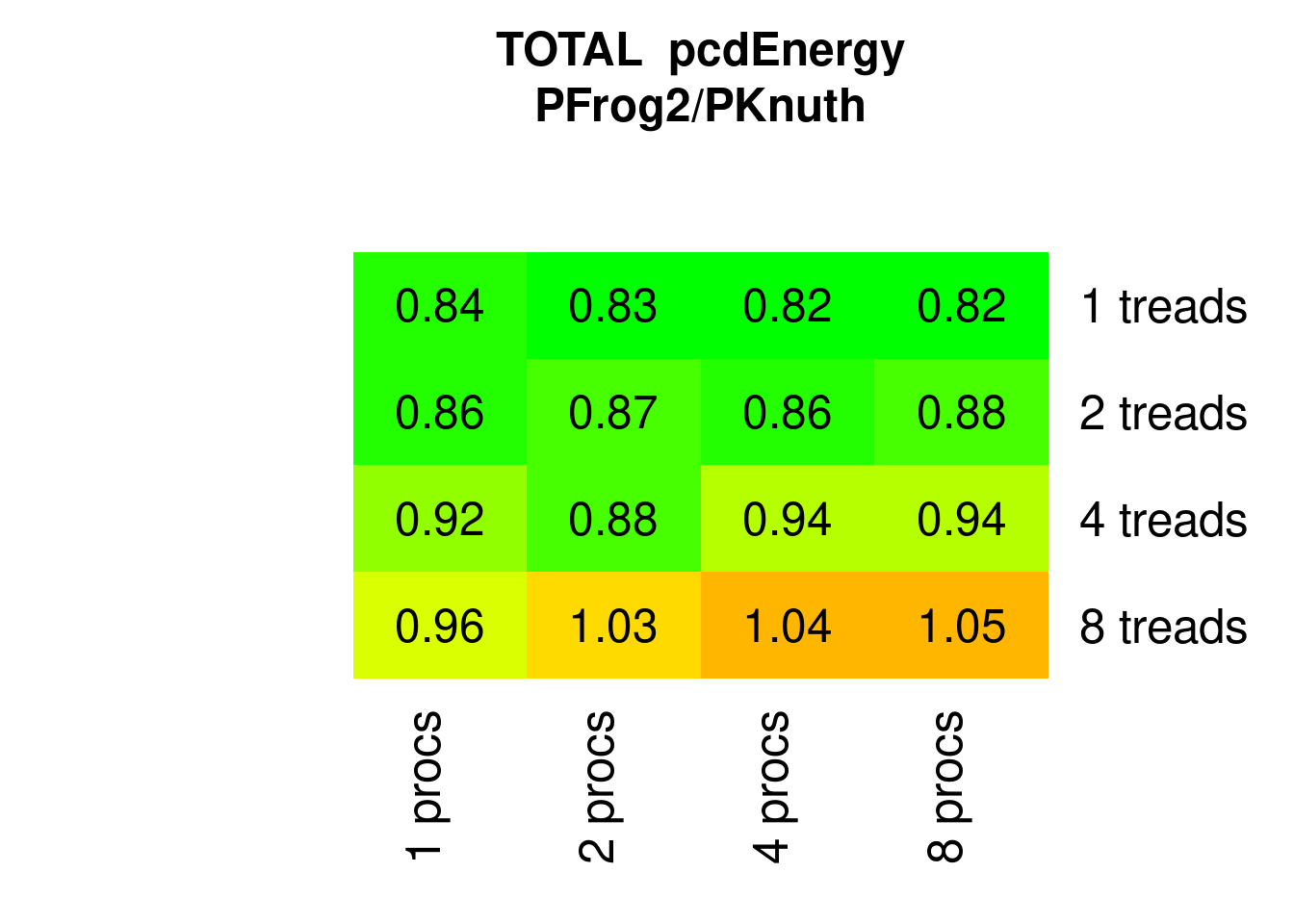
Figure 7.16: Parallel PFrogsort2 Energy relative to Knuthsort
PFrogsort3 tends to need more Energy than PKnuthsort (but less %RAM):
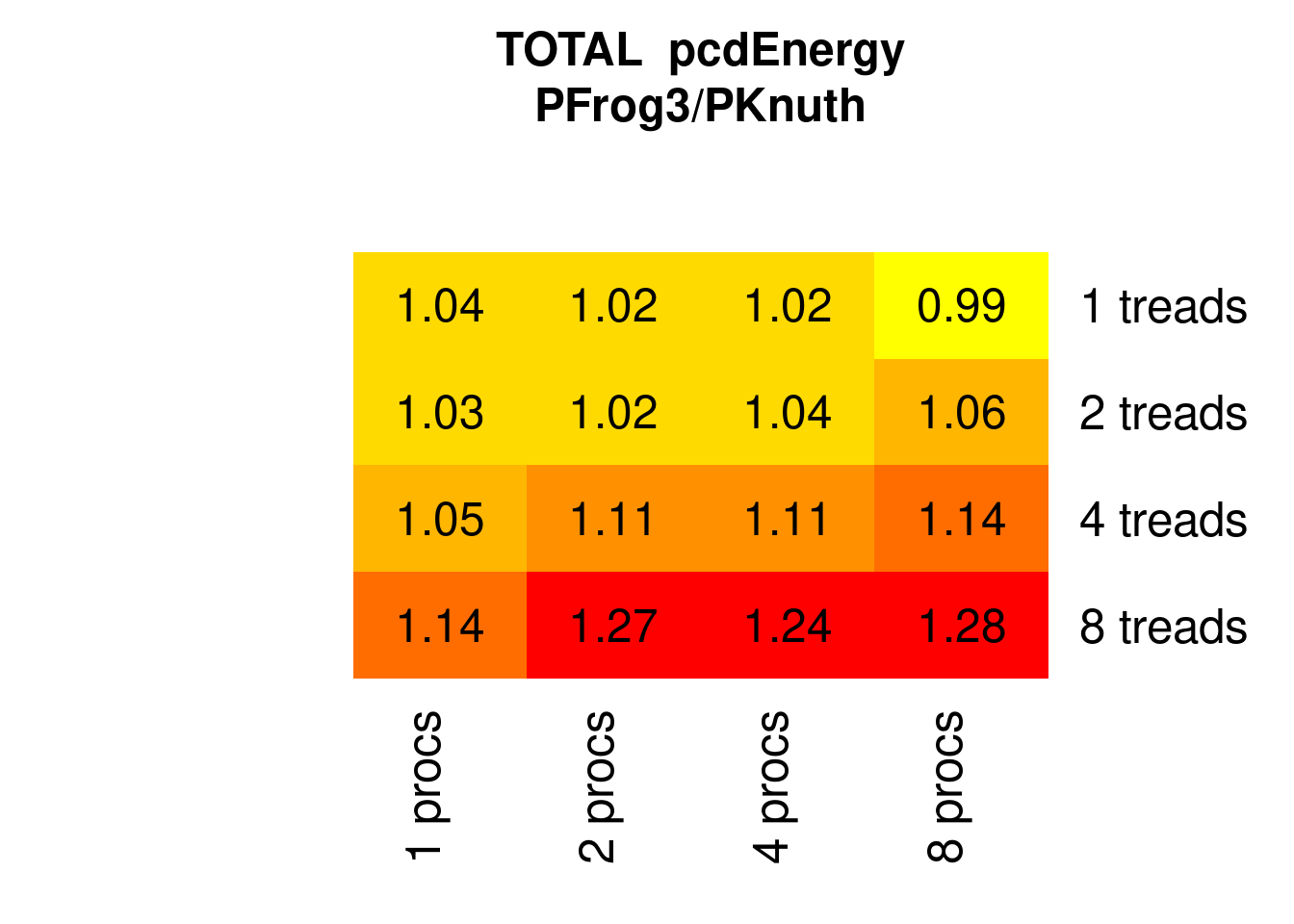
Figure 7.17: Parallel PFrogsort3 Energy relative to Knuthsort
7.1.2.4 Frogsort Footprint
PFrogsort0 and PFrogsort1 have substantially lower eFootprint (about 75%) and PFrogsort2 and PFrogsort3 dramatically lower eFootprint (about 50%, particularly PFrogsort2).
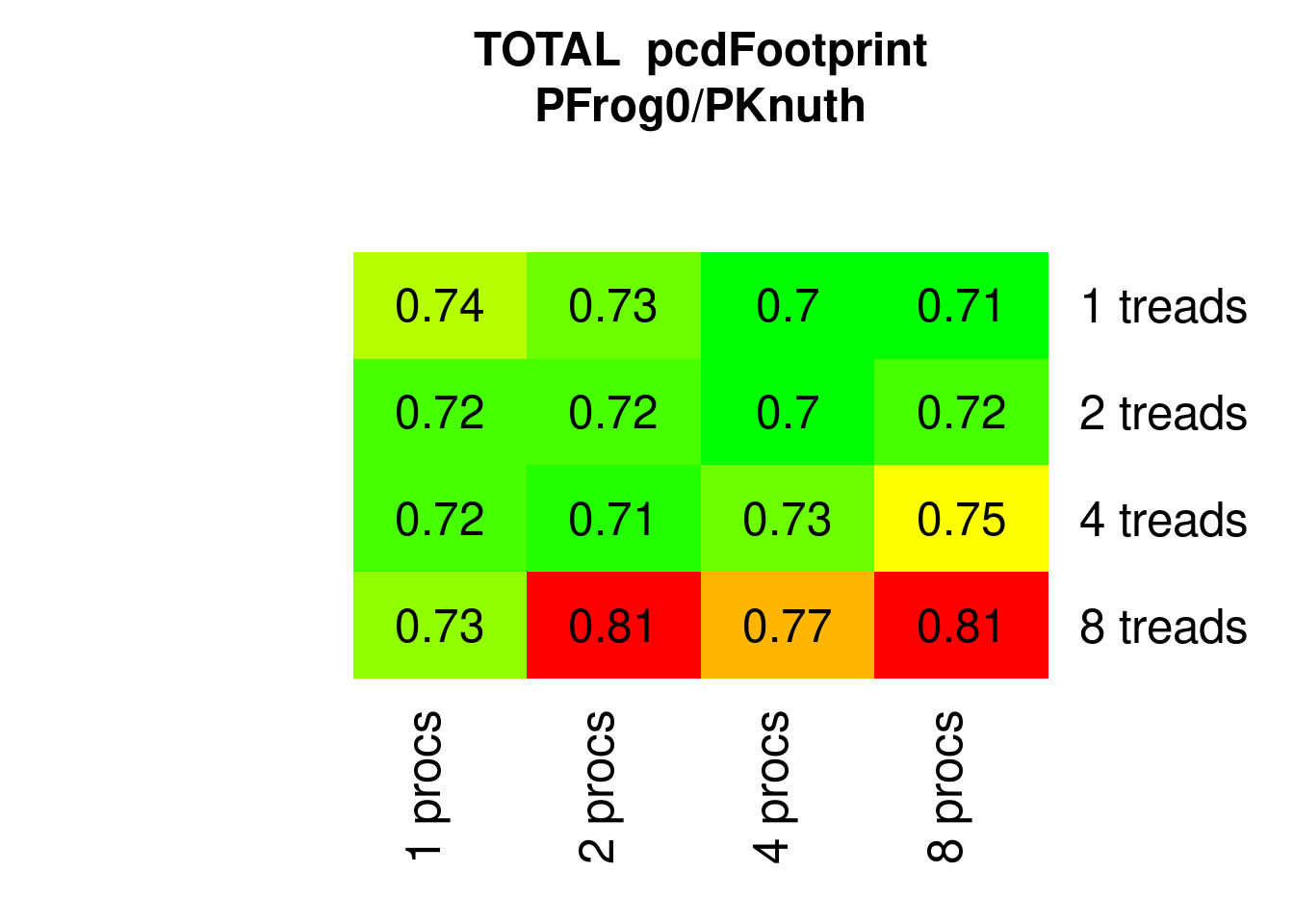
Figure 7.18: Parallel PFrogsort0 eFootprint relative to Knuthsort
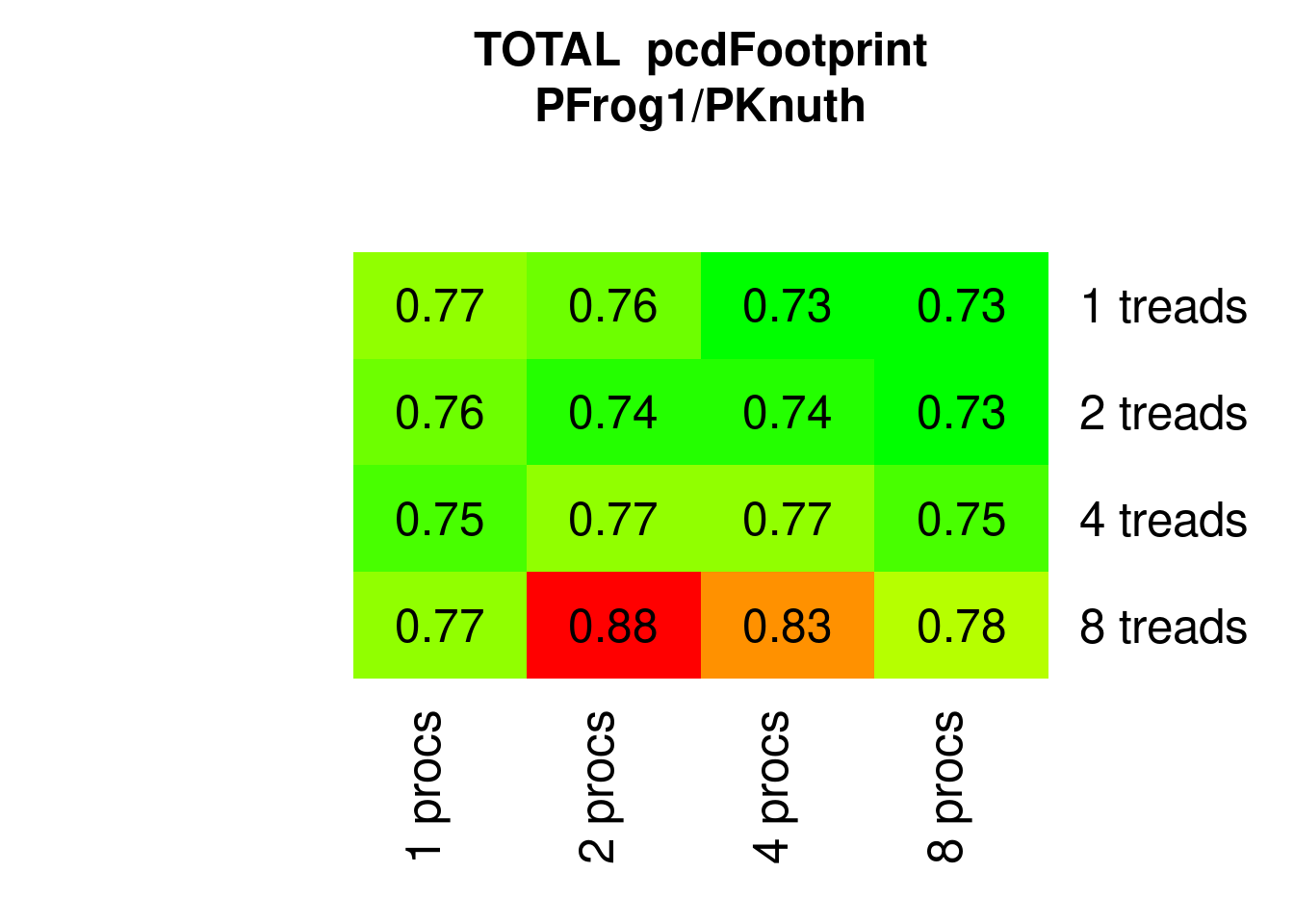
Figure 7.19: Parallel PFrogsort1 eFootprint relative to Knuthsort
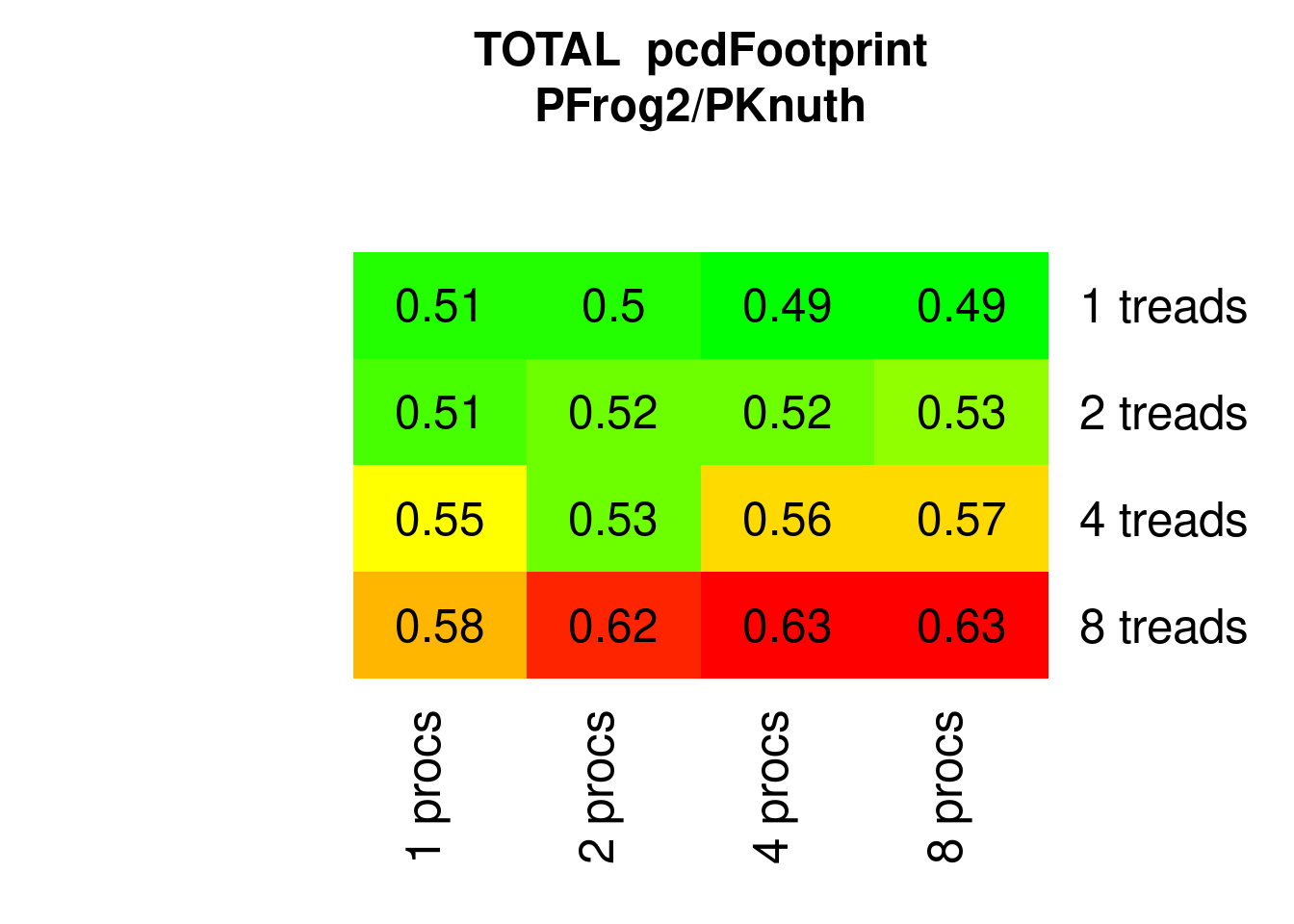
Figure 7.20: Parallel PFrogsort2 eFootprint relative to Knuthsort
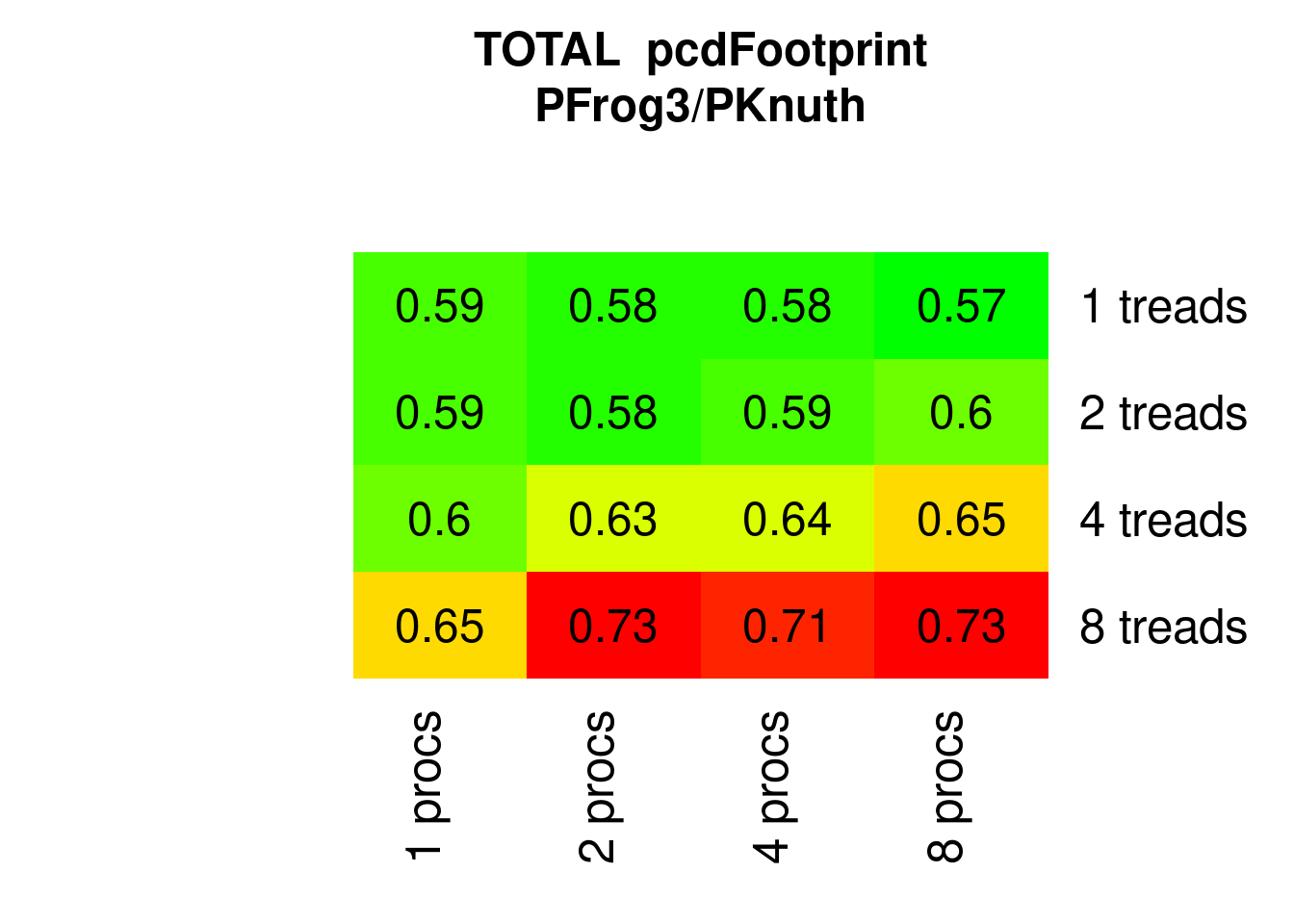
Figure 7.21: Parallel PFrogsort3 eFootprint relative to Knuthsort
In summary, needing less %RAM, the Frogsorts parallelize as well as Mergesorts, they have much lower eFootprint and PFrogsort2 also needs less Energy. The energy (and speed) advantage of PFrogsort2 reduces with more parallel execution, hence it is an open question what happens on CPUs with many more cores.
7.2 Parallel Quicksorts
7.2.1 Quicksort scaling
The parallel Quicksorts use multiple threads only for parallel branches, not for parallel partitioning, hence the expected speedup is lower. Here only the fastest versions with block-tuning are shown, PQuicksort2B and PDucksortB, the two have similar results and don’t benefit from more than 2 threads:
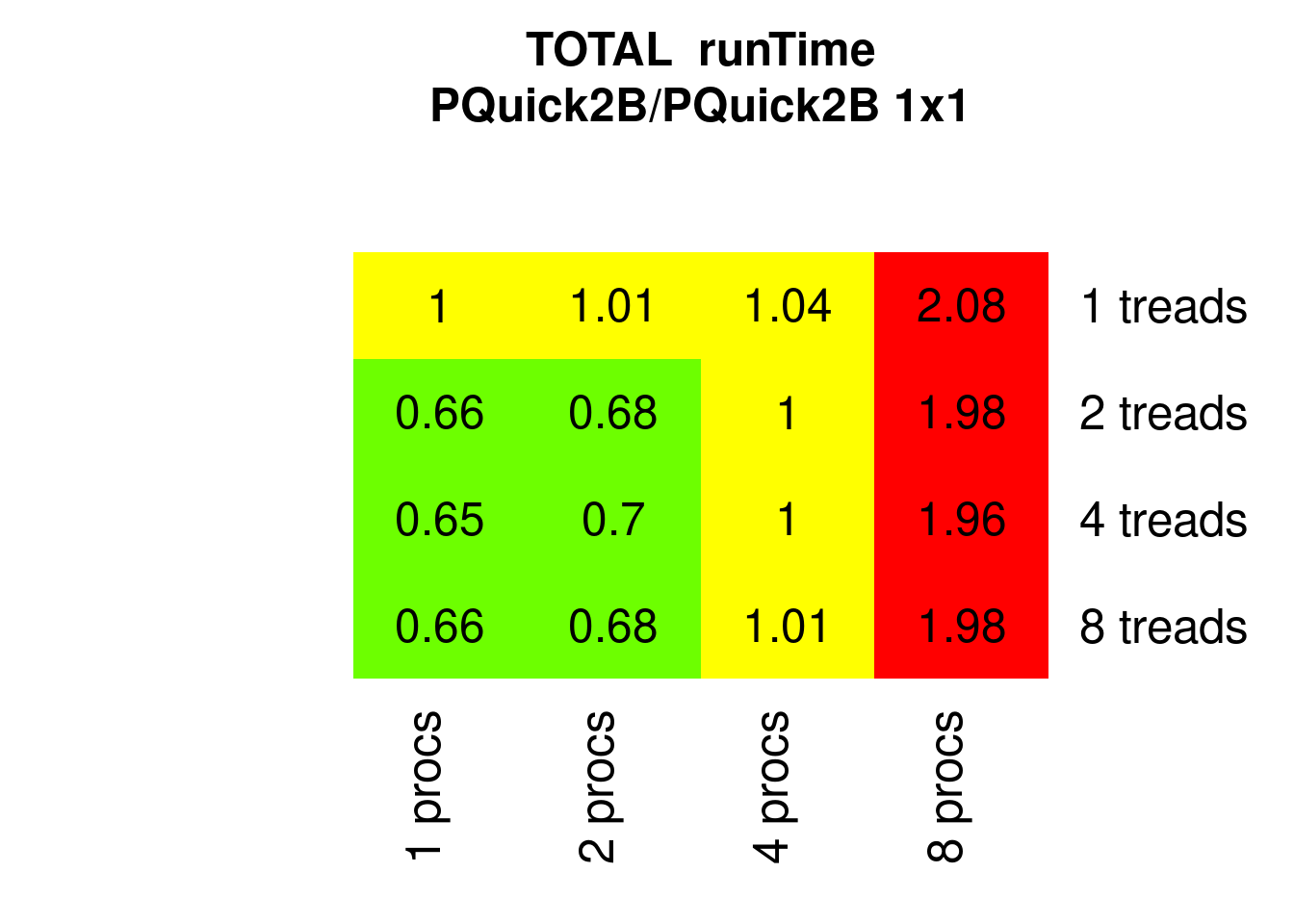
Figure 7.22: Parallel Quicksort2 runTimes relative to 1x1 (1 process 1 thread)
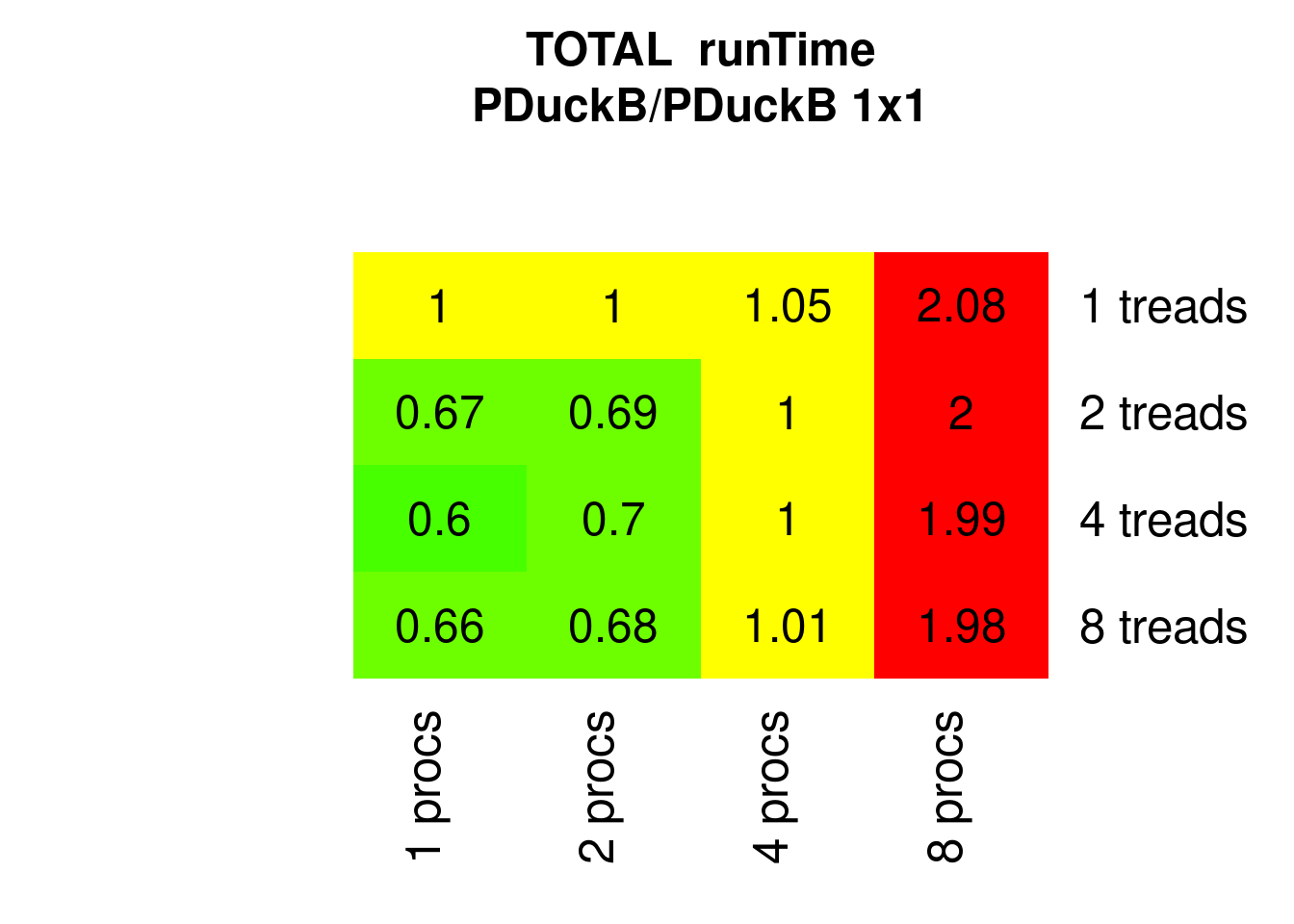
Figure 7.23: Parallel Ducksort runTimes relative to 1x1 (1 process 1 thread)
Note that regarding Energy not even two threads a clearly better than one:
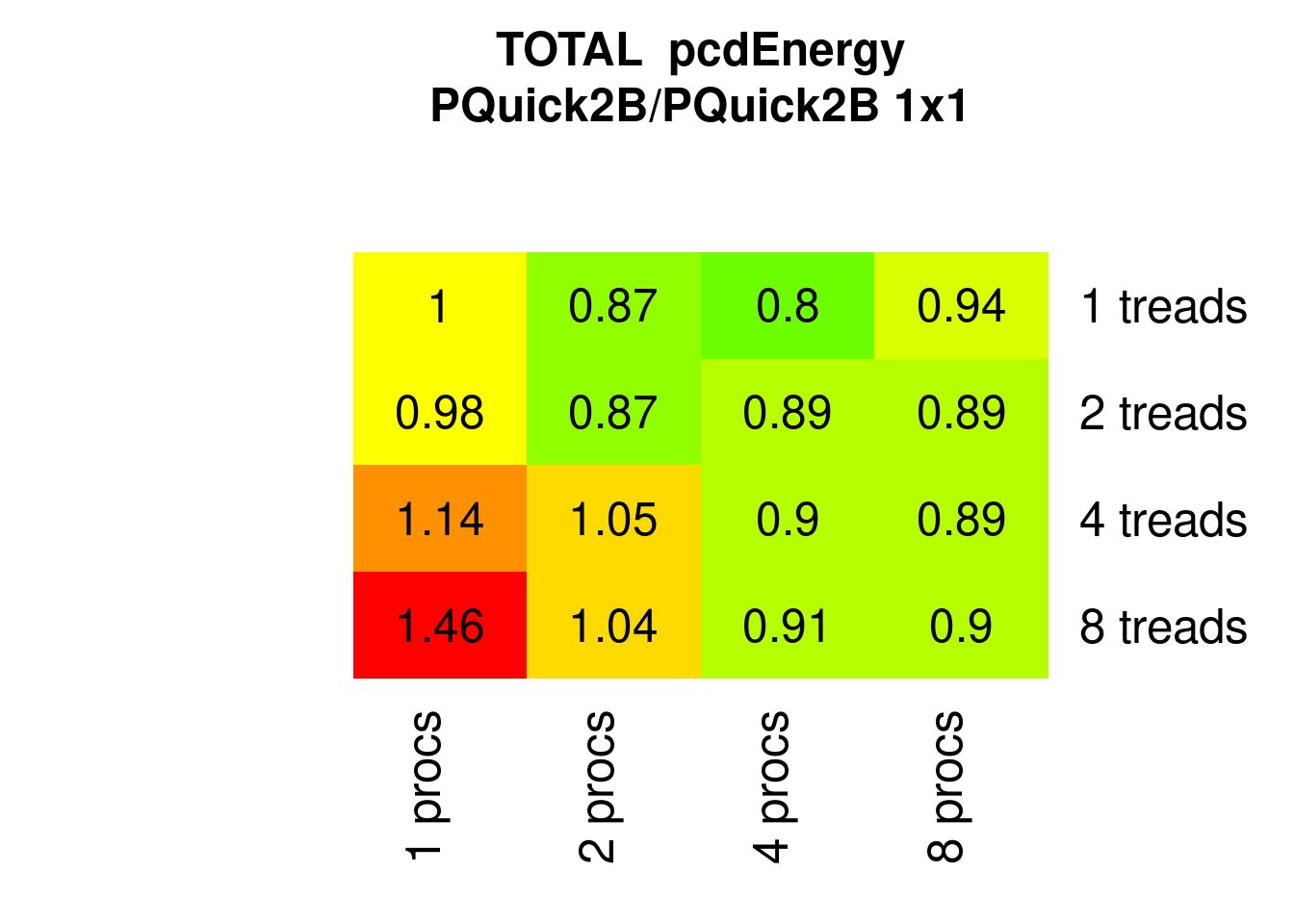
Figure 7.24: Parallel Quicksort2 Energy relative to 1x1 (1 process 1 thread)
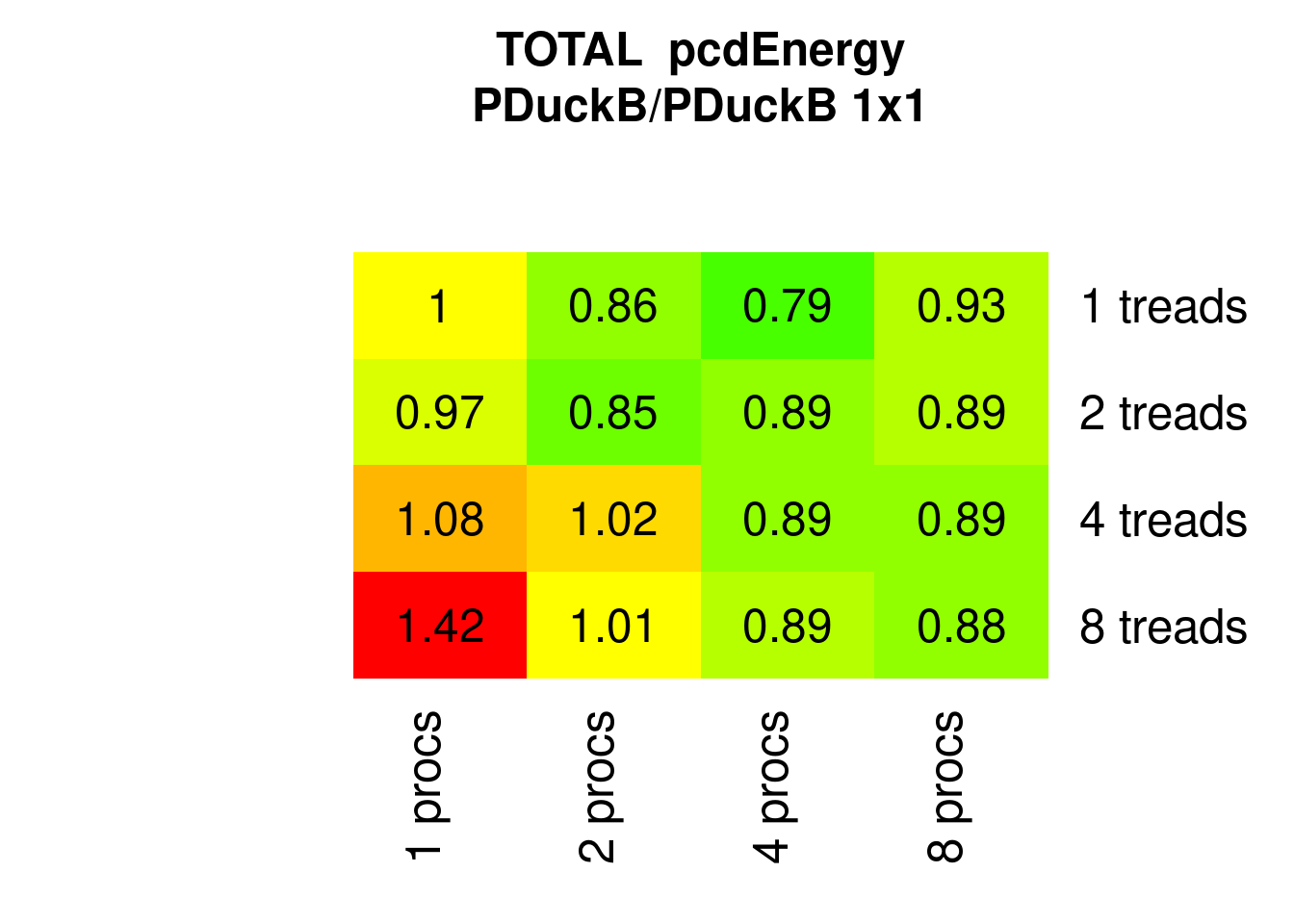
Figure 7.25: Parallel Ducksort Energy relative to 1x1 (1 process 1 thread)
7.2.2 Quicksort compared
PQuicksort2 is faster than PKnuthsort, except for high multi-threading and low parallel processes:
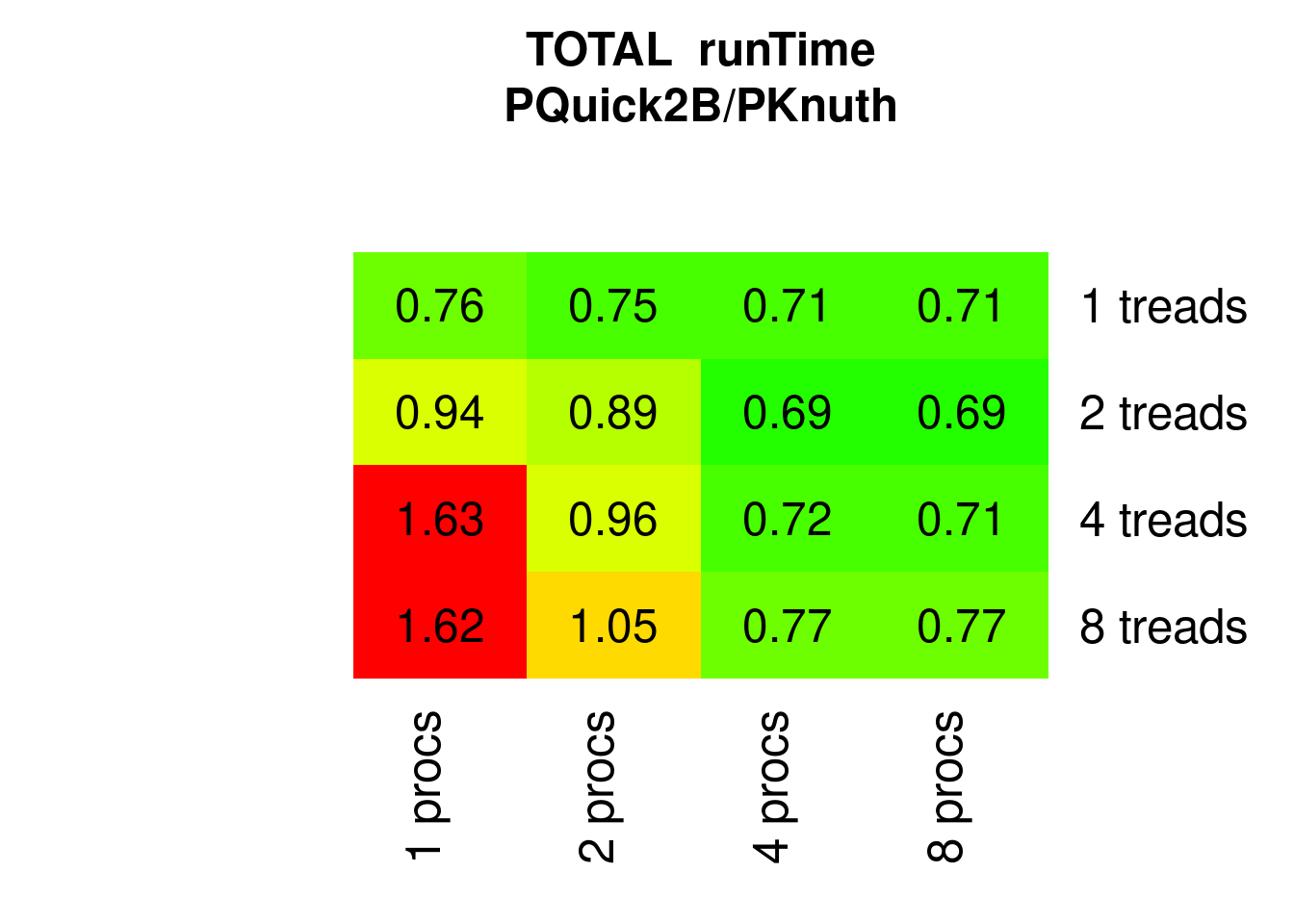
Figure 7.26: Parallel Quicksort2 speed relative to parallel Knuthsort)
PDucksortB does a bit better, but expectedly shows the same pattern:
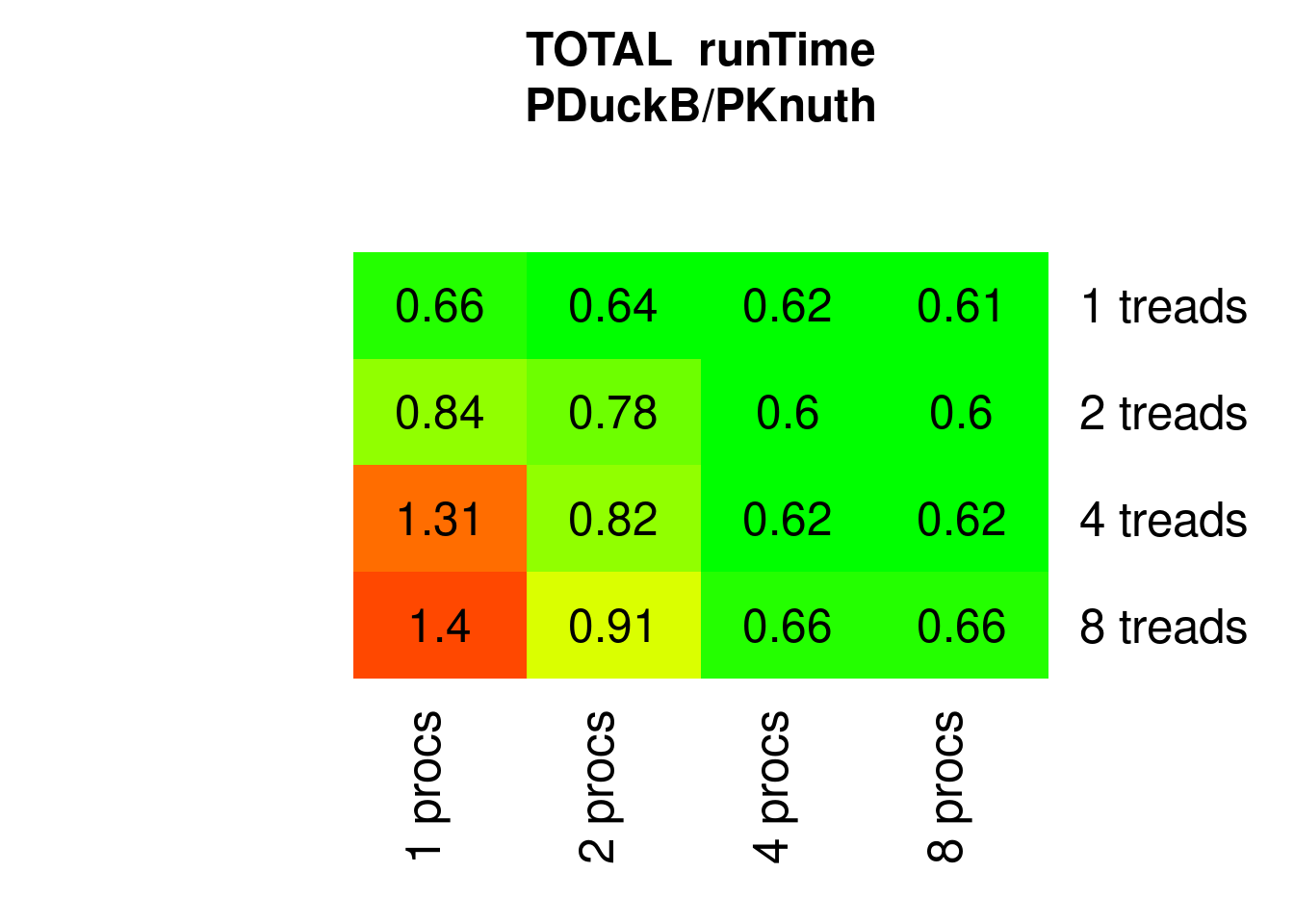
Figure 7.27: Parallel Ducksort (block-tuned) speed relative to parallel Knuthsort
Now comparing for Energy against PKnuthsort: if applicable and not multi-threaded too much PQuicksort2B saves 25% to 33%:
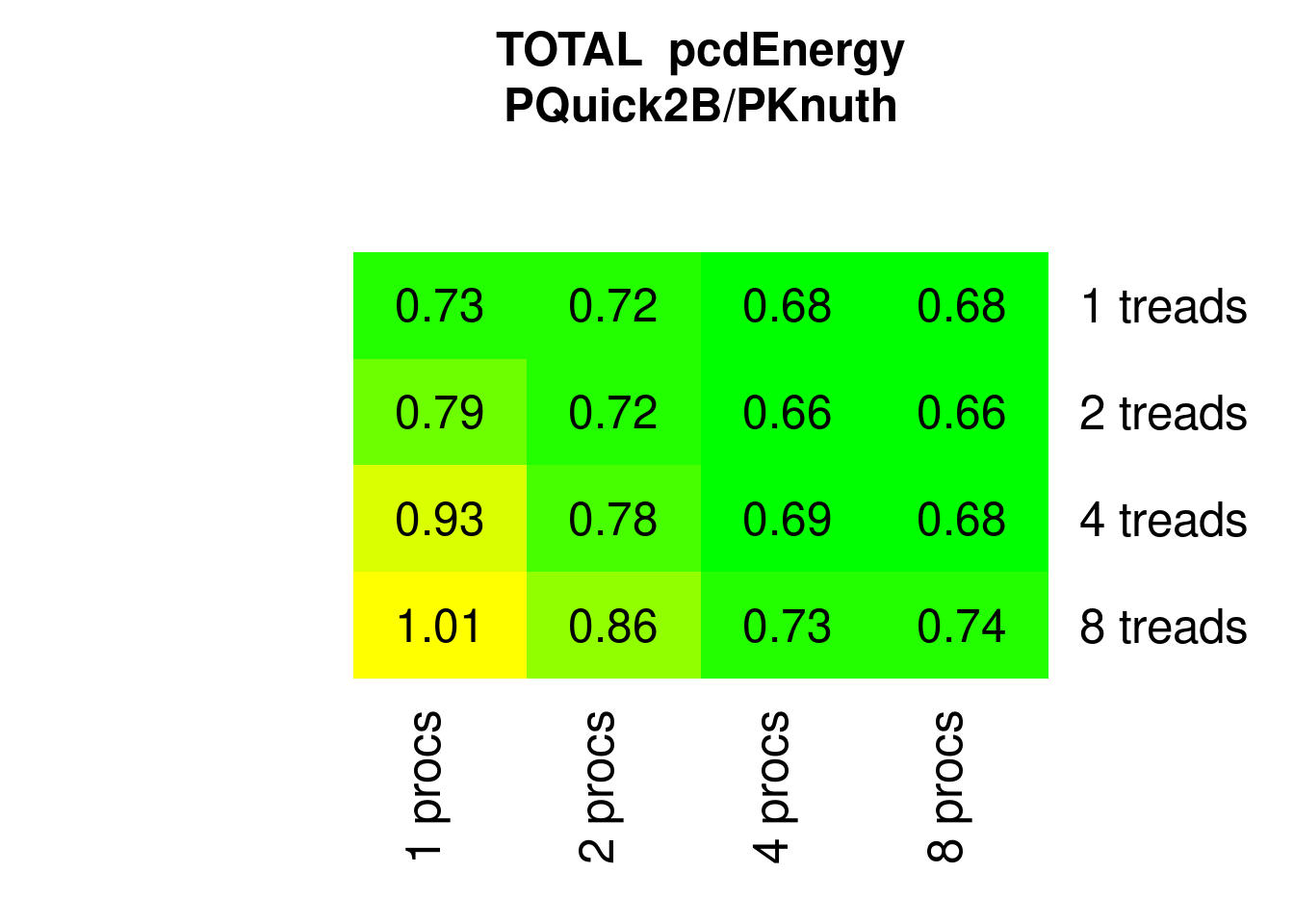
Figure 7.28: Parallel Quicksort2 Energy relative to parallel Knuthsort)
PDucksortB saves even more (35% to 40%):
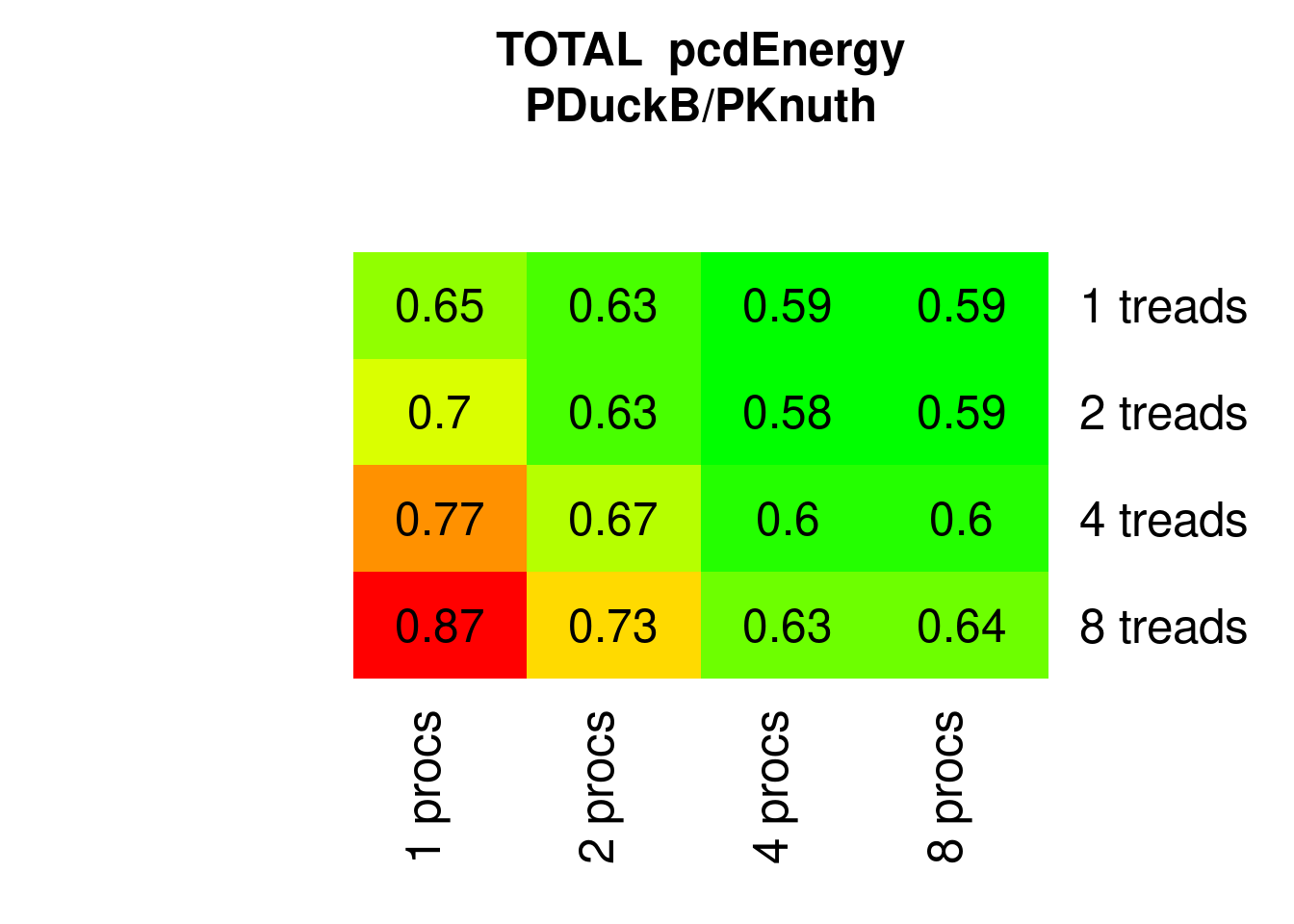
Figure 7.29: Parallel Ducksort Energy relative to parallel Knuthsort
Regarding eFootprint against PKnuthsort, the savings are dramatic, about 66%:
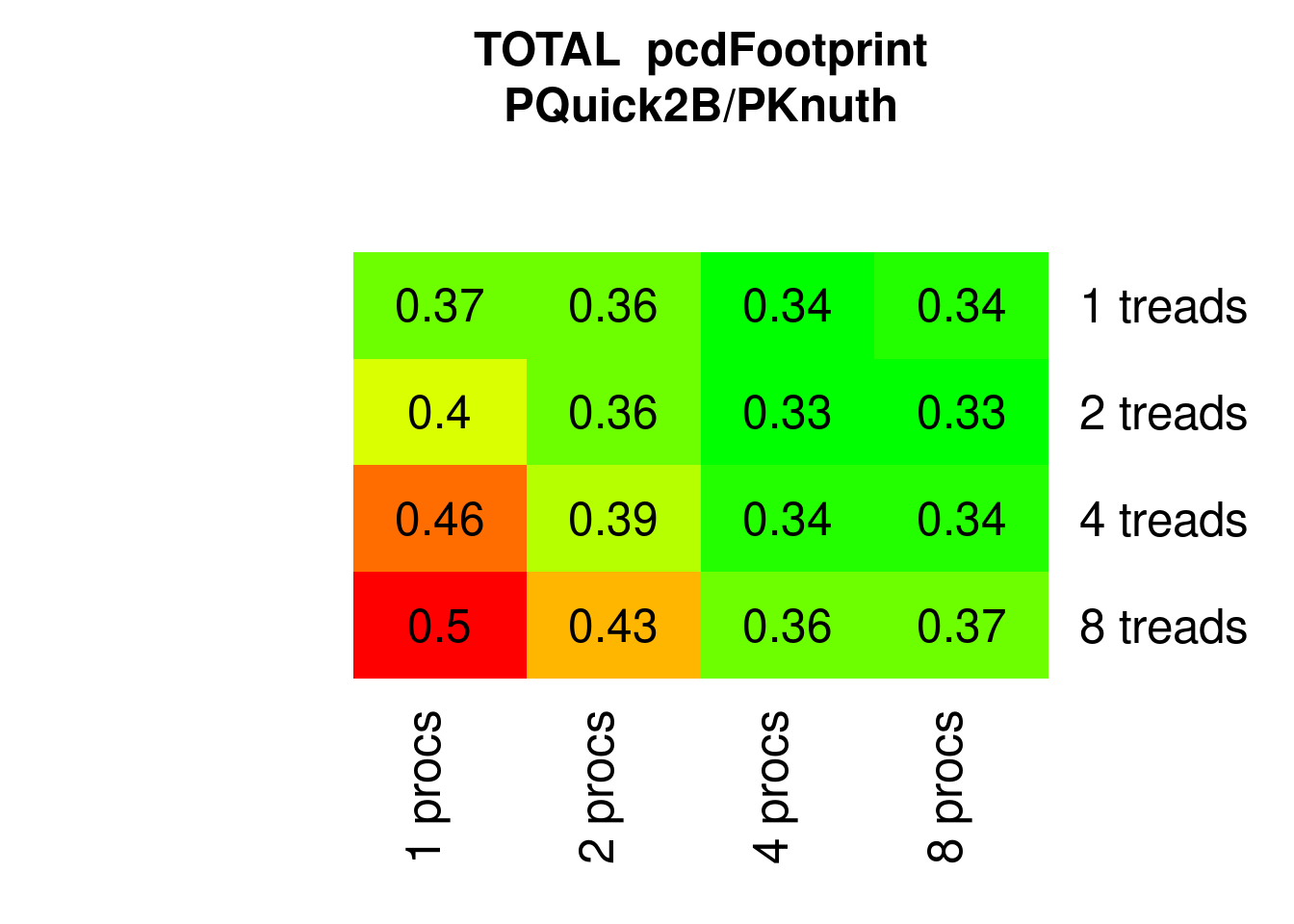
Figure 7.30: Parallel Quicksort2 eFootprint relative to parallel Knuthsort
PDucksort is even better:
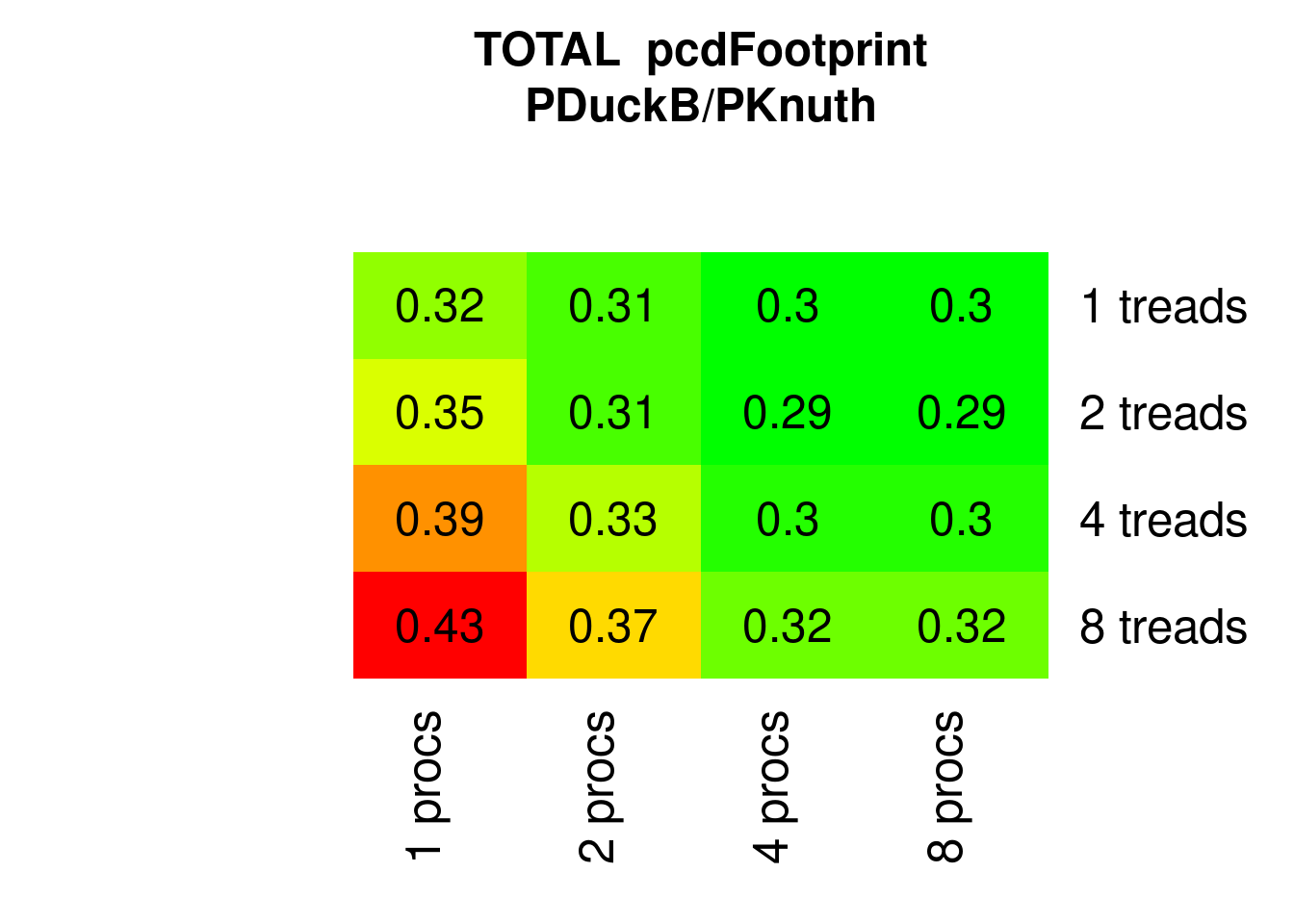
Figure 7.31: Parallel Ducksort eFootprint relative to parallel Knuthsort
In summary, partial parallelization of the Quicksorts gave some speed benefits, but neither achieves the speed of the parallel Mergesorts, nor achieves Energy benefits compared to serial execution. However, at 4 physical cores, regarding Energy and particularly regarding eFootprint the Quicksorts are still much better than the Mergesorts (provided they are applicable).
7.3 Update: AMD
Here I report some results with the 8-core AMD® Ryzen 7 pro 6850u (single runs with n=2^27), which gives quite similar results: Frogsort0 scales as well as Knuthsort: both achieve speedup factor 8 with 16 hyper-threads. Frogsort2 - after parallelizing some previously serial subtasks - achieves speedup factor 7.5 ex-situ and still factor 6.5 in-situ (results shown here are in-situ).

Figure 7.32: Scaling of parallel algorithms (runTime). (K)nuthsort (F)rosgsort0 Frogsort(2) (Q)uicksort2B
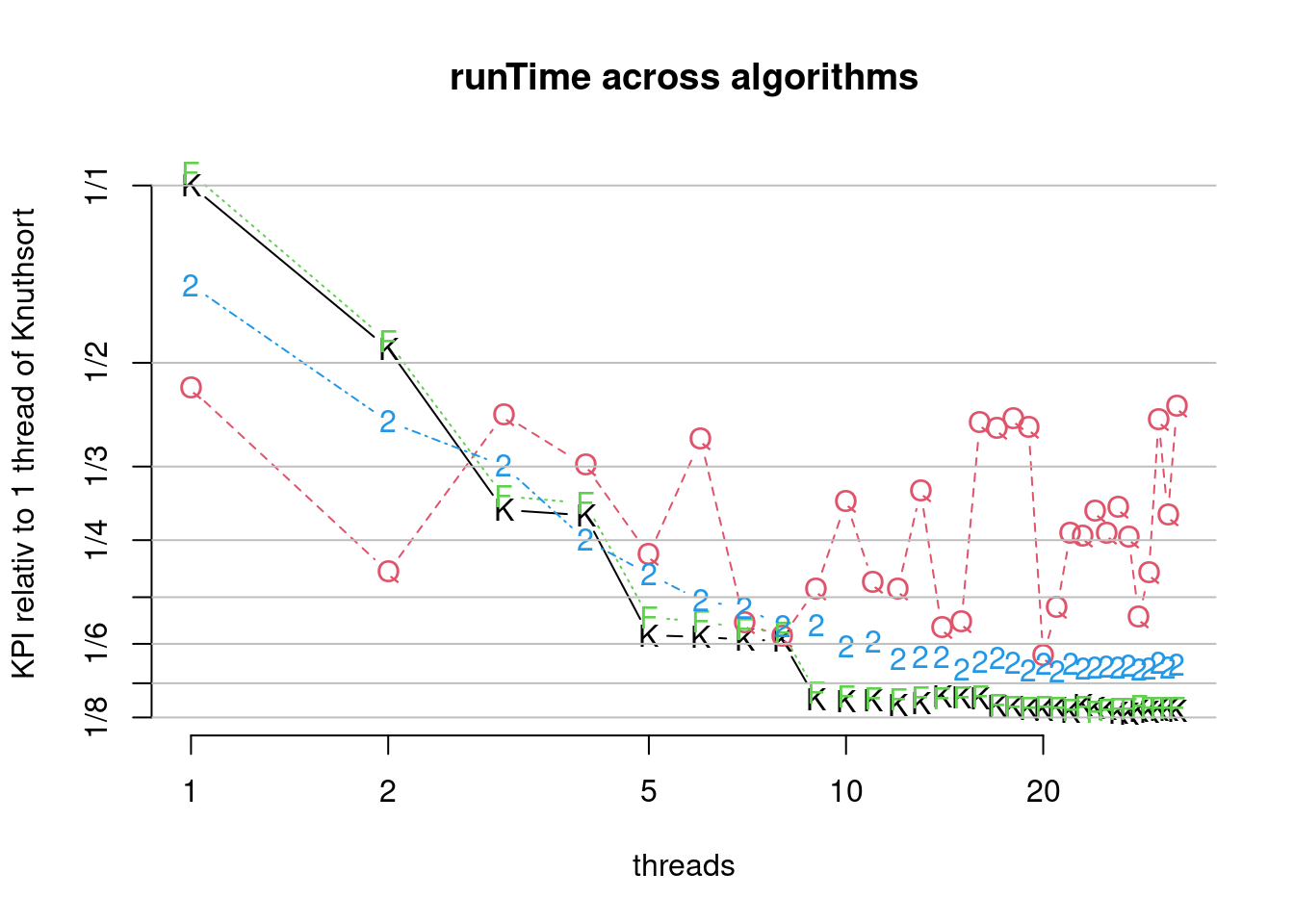
Figure 7.33: Comparison of parallel algorithms (runTime). (K)nuthsort (F)rosgsort0 Frogsort(2) (Q)uicksort2B
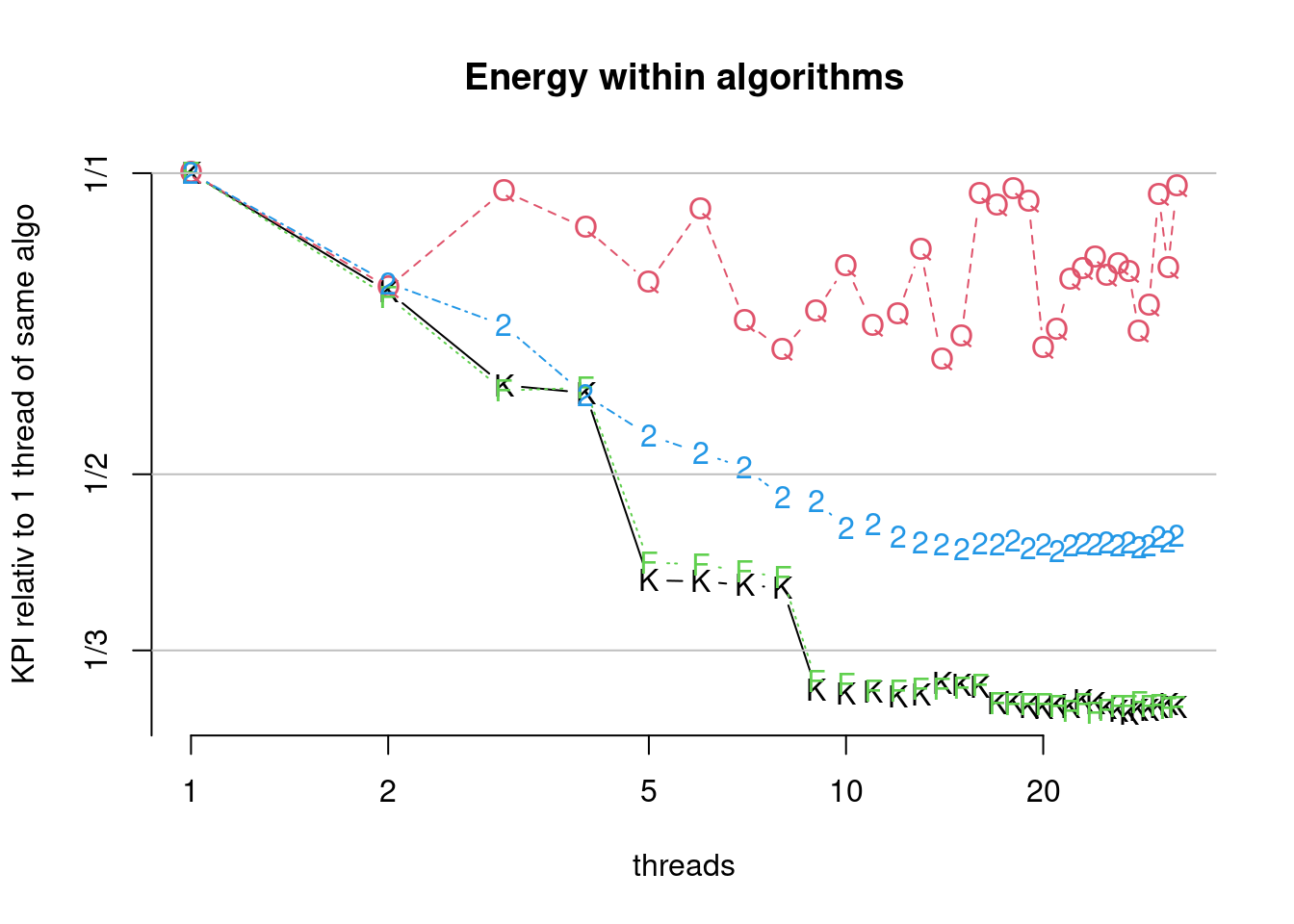
Figure 7.34: Scaling of parallel algorithms (bcdEnergy). (K)nuthsort (F)rosgsort0 Frogsort(2) (Q)uicksort2B
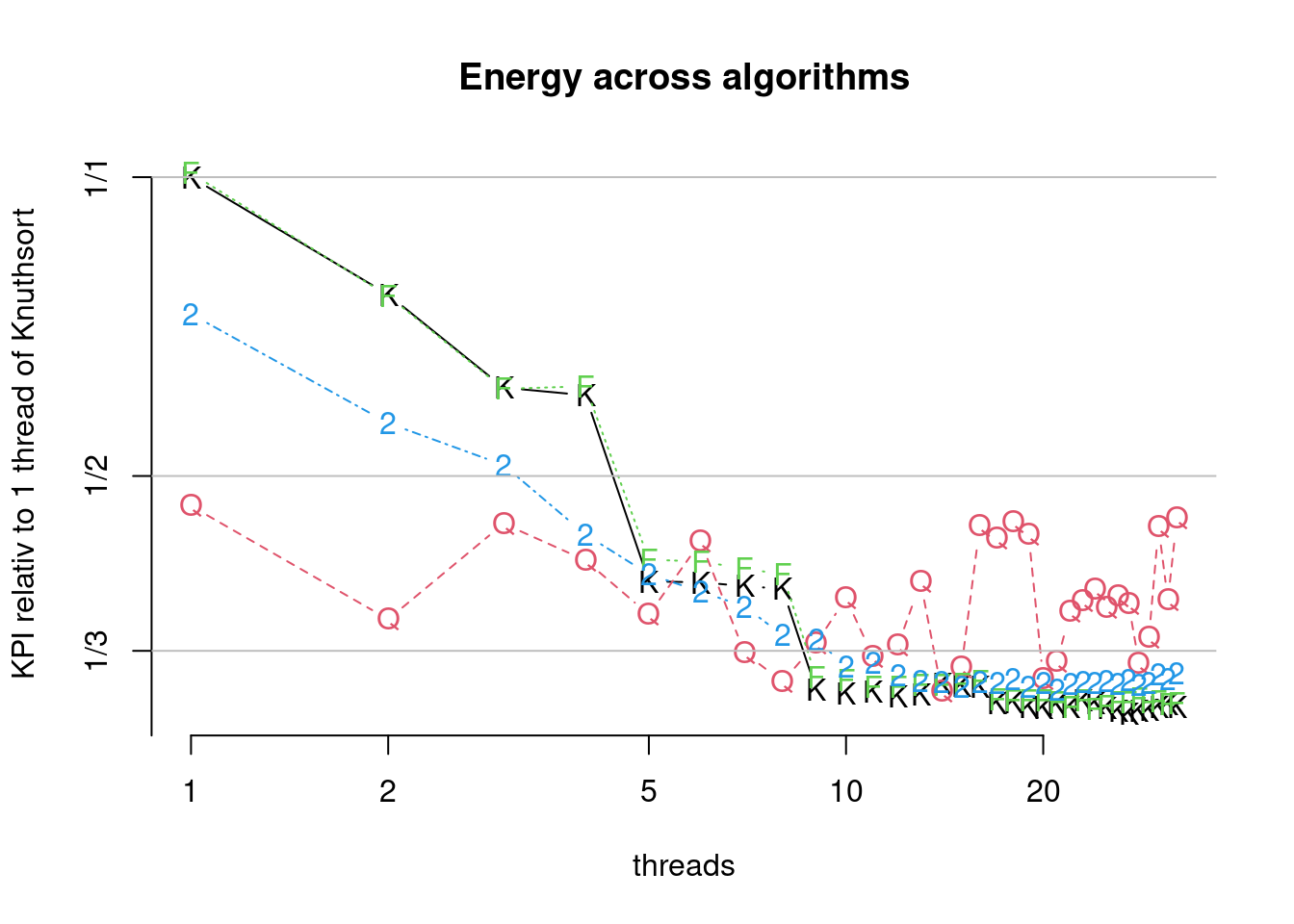
Figure 7.35: Comparison of parallel algorithms (bcdEnergy). (K)nuthsort (F)rosgsort0 Frogsort(2) (Q)uicksort2B
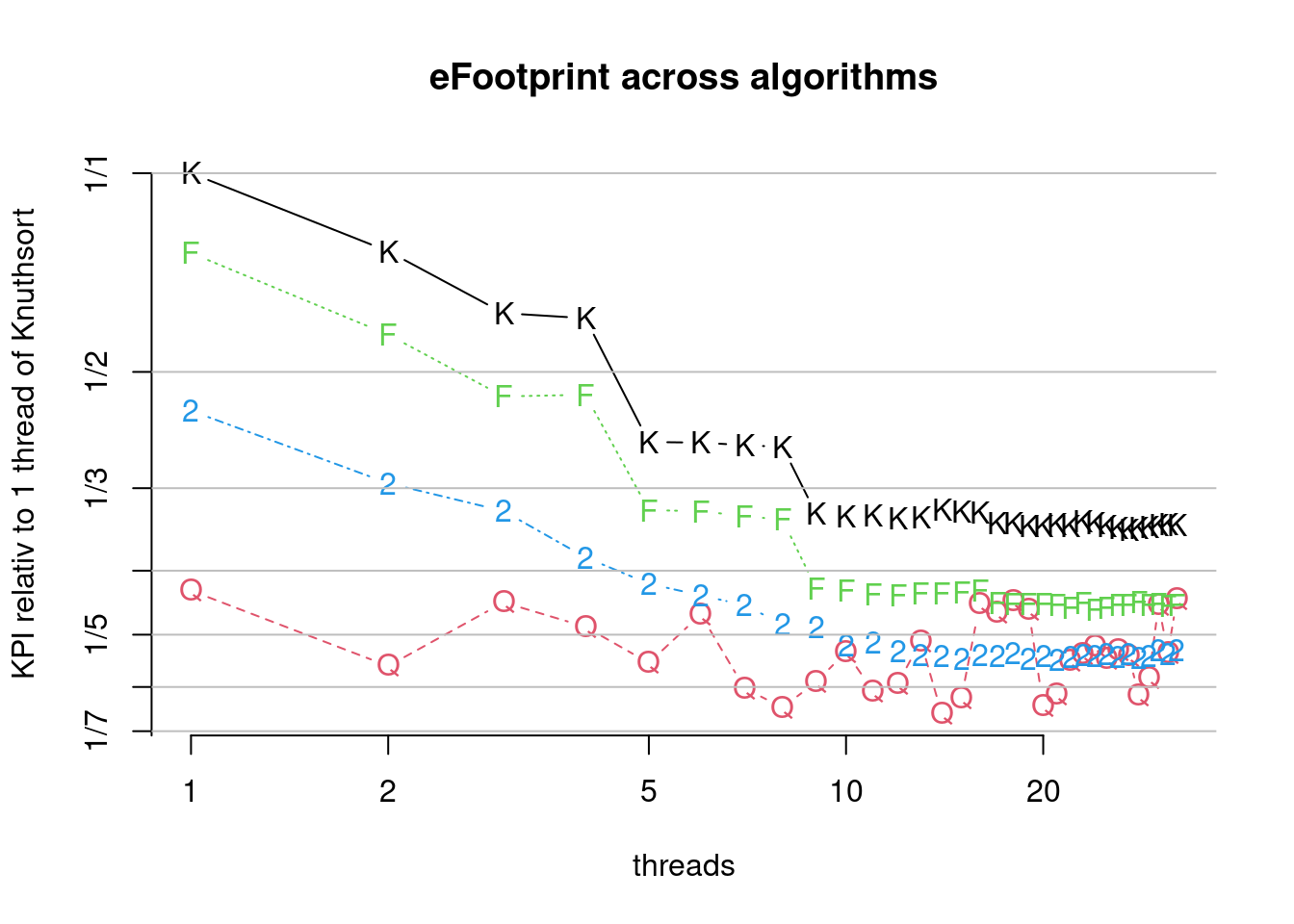
Figure 7.36: Comparison of parallel algorithms (bcdFootprint). (K)nuthsort (F)rosgsort0 Frogsort(2) (Q)uicksort2B
7.4 Parallel conclusion
Parallelization can save Energy, by running multiple concurrent tasks, by multi-threading tasks or by both.
The results have shown that the greeNsort® algorithms - despite their lower memory-requirements - can be multi-threaded as well as their prior art counterparts. greeNsort® Split&Merge algorithms have lower eFootprint than their prior art counterparts, and some even need less Energy or less RUNtime.
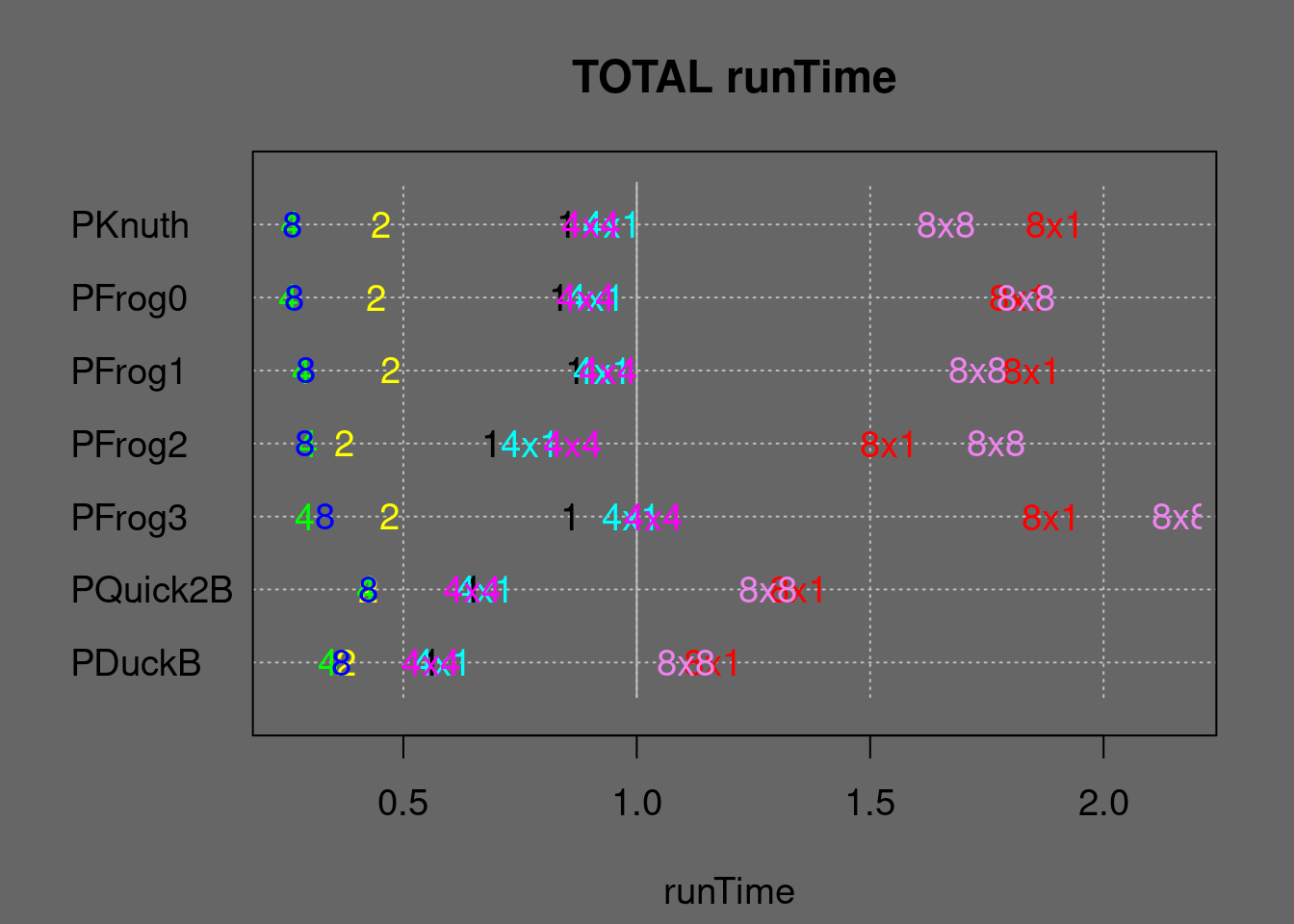
Figure 7.37: runTime summary of parallel algorithms
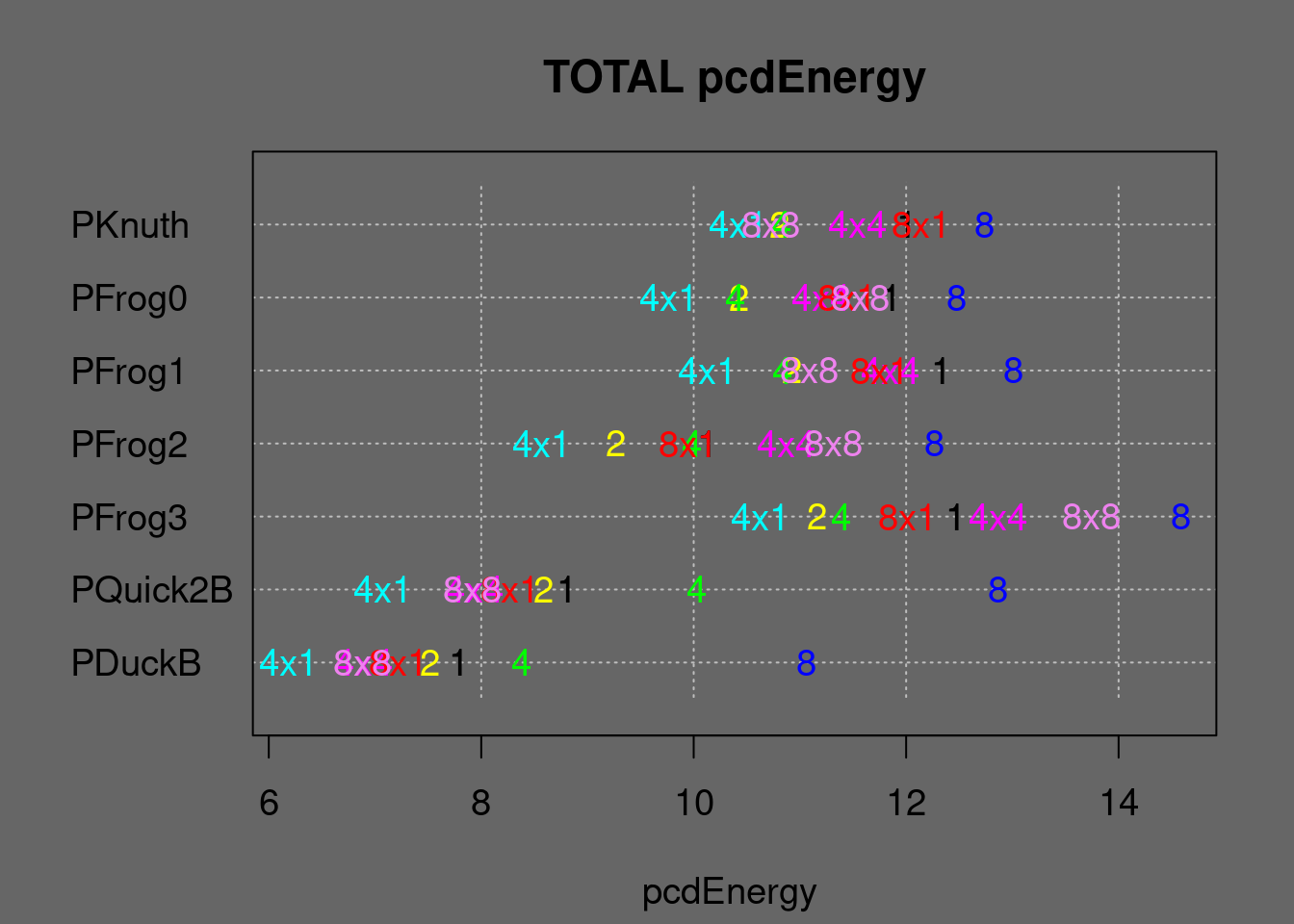
Figure 7.38: Energy summary of parallel algorithms
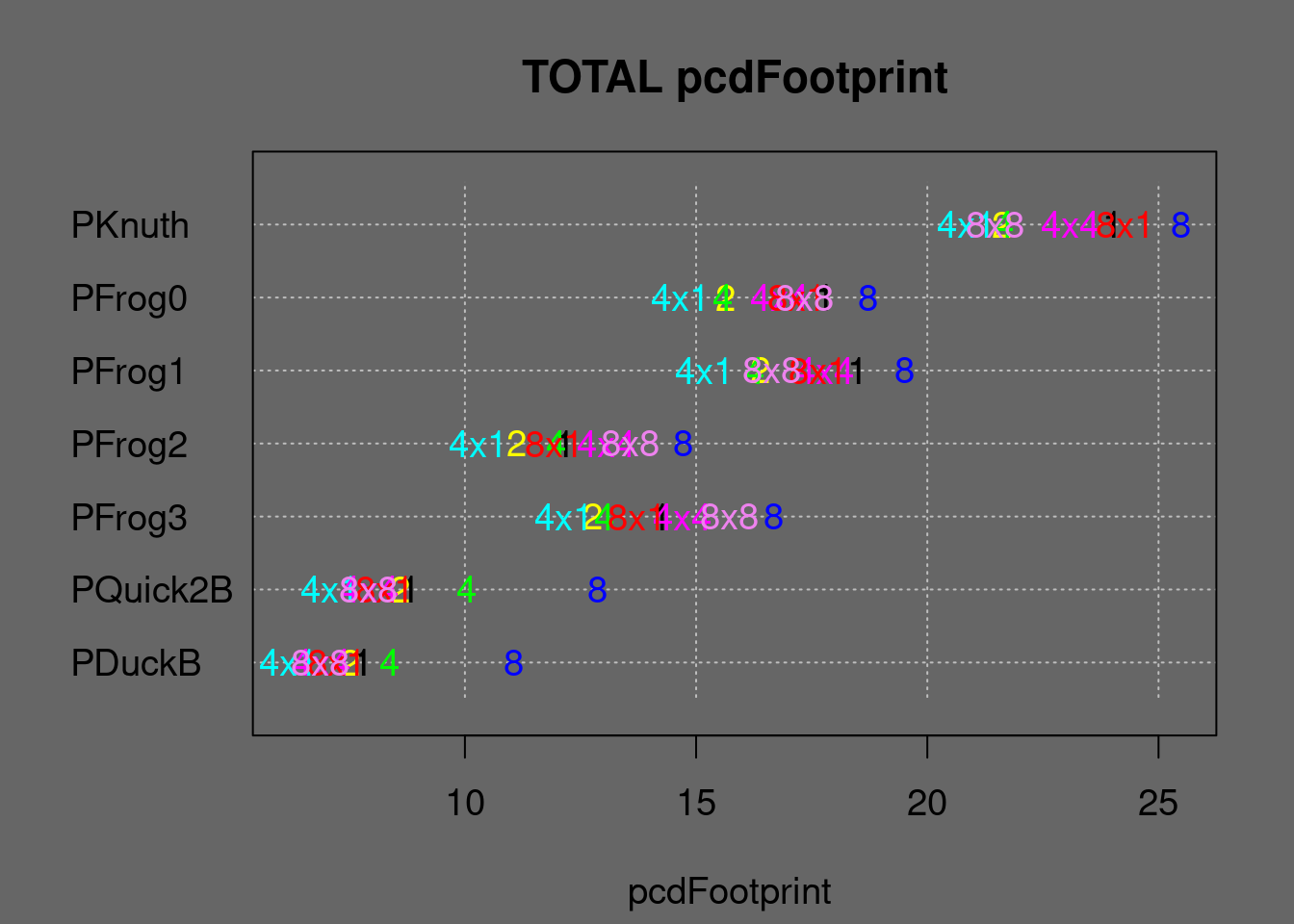
Figure 7.39: eFootprint summary of parallel algorithms