Results: greeNsort® delivers huge savings
The greeNsort® in-memory sorting algorithms improve merging, partitioning and introduce a novel class of in-memory sorting algorithms
Better merging
Sorting problems and certain statistical experiments (…) require a memory for the material which is being treated — John von Neumann
The greeNsort® research shows how to construct sorting algorithms based on merging with less memory. Further the greeNsort® research shows that an algorithm based on merging (\(\mathcal{O}(N\log{N})\)) can smoothly be tuned to linear cost for the presorted best-case (\(\mathcal{O}(N)\)) without sacrificing its worst-case performance (when data is unsorted), unlike the the famous Timsort algorithm in Python and Java: it is known to have a linear best-case, less known is that Timsort is dramatically slower than much simpler algorithms when it comes to real sorting tasks (that are not almost presorted).
The greeNsort® algorithms achieve better sustainability than the combined teaching on Mergesort by Donald Knuth, Robert Sedgewick, Jyrki Katajainen, Huang&Langston and Tim Peters. The greeNsort® research completes an open topic since the invention of Mergesort by John von Neumann in 1945.
Better partitioning
There are two ways of constructing a software design: One way is to make it so simple that there are obviously no deficiencies, and the other way is to make it so complicated that there are no obvious deficiencies. The first method is far more difficult. — Sir Charles Antony Richard Hoare
The greeNsort® research shows that an algorithm based on partitioning (\(\mathcal{O}(N\log{N})\)) can smoothly be tuned to linear cost for the best-case of purely tied keys (\(\mathcal{O}(N\log{d})\), where d is the number of distinct values) without sacrificing its worst-case performance (when all keys are distinct hence no ties). The famous 3-way-Quicksort3 algorithm early-terminates on ties but pays the price of extra-operations in the worst-case compared to the simpler binary Quicksort2 .
The greeNsort® algorithms achieve \(\mathcal{O}(N\log{d})\) early termination without extra overhead, unlike the Quicksort algorithms taught by R. C. Singleton (1969), Robert Sedgewick (1977), Wegner (1985) and Bentley&McIlroy (1993), Vladimir Yaroslavskiy (2009) and Edelkamp&Weiß (2016)1. The greeNsort® research hence completes an open topic since the invention of Quicksort by C. A. R. Hoare in 1961.
Theory: a new algorithmic class
The psychological profiling [of a programmer] is mostly the ability to shift levels of abstraction, from low level to high level. To see something in the small and to see something in the large. — Donald Knuth
The greeNsort® research has developed a new class of algorithms spanning merging and partitioning
- some embodiments are simple and elegant
- some embodiments are robust and adaptive
- some embodiments are more sustainable than the prior-art: have better trade-offs between speed (energy) and memory requirements (hardware)
- some embodiments are more adaptive than the prior-art: have better trade-offs between worst-case and best-case performance
Software: validated C-code
Beware of bugs in the above code; I have only proved it correct, not tried it. — Donald Knuth
Without the genius of Donald Knuth we’d better verify our conclusions, even correct proofs can be based on wrong assumptions. Our testbed includes 65 greeNsort® algorithms and 50 prior-art algorithms of comparable implementation quality2 written in C. The code is bundled in a well-documented R-package with 53 synthetic data generators and 17 data generators for natural language strings of varying size, in particular:
- all implementations are single threaded (however, greeNsort® algorithms are designed for parallel execution)
- most implementations are binary algorithms (with a few 3-ary and 4-ary exceptions)
- the algorithms have been tested on numerous data patterns
- the algorithms have been tested for correctness (and stable ones for
correct stability)
- the algorithms have been tested for performance (they return their runtime, memory and footprint)
- the algorithms have been tested for correct memory access through
the Valgrind checker
- the algorithms have been validated by Intel RAPL energy measurements
- the algorithms have been validated against numerous prior-art algorithms
Empirics: huge savings potential
Above all else show the data — Edward Tufte
The best greeNsort® algorithms have been compared against the best prior-art algorithms for a couple of important sorting disciplines, for details see the greeNsort® portfolio. The available greeNsort® portfolio of algorithms delivers faster sorting with less hardware. Depending on the sorting discipline greeNsort® algorithms save 3% to 40% of sorting time and energy. greeNsort® algorithms allow switching to more sustainable sorting disciplines because they deliver competitive speed while saving up to 50% of hardware memory. The results for stable sorting on a mix of real-world data situations are shown in the following.
The prior-art shows a typical space-time trade-of from Grailsort (Grail: 0% buffer) being slowest, over Sqrtsort (Sqrt: almost 0% buffer) and Timsort3 (Tim: 50% buffer) to Mergesort (Knuth: 100% buffer) being fastest. The greeNsort® algorithms are consistently faster than the prior-art given equal amount of buffer. Note that Frogsort2 and Squidsort2 can sort faster and with less memory than the prior-art when given between 5% and 45% buffer. Note further that Walksort is even faster than Timsort although it requires almost no buffer. Finally note that Octosort like Timsort achieves linear cost for presorted data but without sacrificing speed on difficult sorting tasks: it’s as fast as Mergesort.
Memory vs. Runtime trade-off for stable sorting algorithms on real-world-data: average measurement on ascglobal + asclocal + tieboot + tiesqrt datasets; red=prior-art, violet=Squid2, cyan=Frog3, green=Frog2 and other greeNsort® algorithms.
Memory vs. Footprint trade-off for stable sorting algorithms on real-world-data: average measurement on ascglobal + asclocal + tieboot + tiesqrt datasets; red=prior-art, violet=Squid2, cyan=Frog3, green=Frog2 and other greeNsort® algorithms.
How much the greeNsort® algorithms are better can bee seen when looking at the fair Footprint measure instead of Runtime (the latter favors algorithms using much memory whereas the former gives a fair comparison): Compared to the fastest Mergesort (Knuth) the best greeNsort® algorithm (Frog2) reduces the footprint by about 50% (and is faster), compared to Timsort the footprint is reduced by about 40% and even compared to Sqrtsort4 the footprint reduction is about 30%.
Deep dive: multi-threading
We call this the race to idle. The faster we can complete the workload and get the computer back to idle, the more energy we can save. — Intel5
Multi-threading not only delivers better performance but also better energy-efficiency. If we can achieve this with less hardware and embedded carbon: all the better. However, in some systems such as latency-critical servers we do not want a single session do grab all available hardware threads, there we want one or just a few threads. Hence both is important: efficient single-threaded and multi-threaded execution. greeNsort® algorithms match the prior art in multi-threaded efficiency, beat the prior-art in single-threaded efficiency and require less memory hence less embedded energy in the hardware.
In the following we compare multi-threaded implementations of Mergesort (Knuth’s merge), Frogsort0, Frogsort1, Frogsort2 and Frogsort3. Mergesort needs 100% buffer, Frogsort0 needs 50% buffer, Frogsort2 is used with 14% buffer and Frogsort3 is used with 12.5% buffer, the lowest hardware-need hence allowing the most sustainable use of aged computers. For each combination of algorithm and degree of threading we ran 50 experiments with randomly permuted input on a I7-8565U (4-cores, 8 hyperthreads) and excluded the two most extreme outliers.
The first chart shows that regarding runtime our implementation of Mergesort (black) scales very-well with the number of threads used, the same is true for ,Frogsort0 (red), Frogsort1 (blue) and Frogsort3 (cyan). With serial versions Frogsort2 (green) is much faster, this advantage dilutes with increasing number of threads. We can also see what Intel said: multi-threading saves energy (on sufficiently large data sets), here down to about 50%.
Runtime and RAPL energy for 50 experiments - ignoring different memory costs; Mergesort (black), Frogsort0 (grey), Frogsort1 (blue), Frogsort2 (green), Frogsort3 (cyan); ‘0’ marks serial implementations, ‘1’,‘2’,‘4’,‘8’ mark the number of threads in threaded implementations.
The next chart compares Frogsort2 and Quicksort. We see that Quicksort scaling has high variance and rarely achieves an appropriate speed-up (only if random pivots on both branches are equally good and fast and hence avoid waiting). By contrast, Frogsort2 - like all split&merge algorithms - achieves reliably good work-balance and scaling.
Runtime and RAPL energy for 50 experiments - ignoring different memory costs; Quicksort (left), Frogsort2 (right); ‘0’ (grey) marks serial implementations, ‘1’ (black),‘2’ (red),‘4’ (blue) and ‘8’ (green) mark the number of threads in threaded implementations; horizontal lines show median energy of Quicksort2
Now we compare just the most important algorithms just for serial and maximally multithreaded runs. Regarding runtime and energy Frogsort2 is the clear winner in serial sorting, for parallel sorting Frogsort2 is almost as good as Mergesort and clearly better than Quicksort.
Runtime and RAPL energy for 50 experiments - ignoring different memory costs; Mergesort (black), Quicksort(red) and Frogsort2 (green); ‘0’ marks serial implementations, ‘1’,‘2’,‘4’,‘8’ mark the number of threads in threaded implementations; dashed lines show medians of all six groups.
Regarding footprint and efootprint Frogsort2 is the clear winner in serial and parallel sorting over Mergesort and Quicksort, hence achieves the most sustainable combination of runtime energy and hardware cost.
Runtime and RAPL energy for 50 experiments - considering different memory costs; Mergesort (black), Quicksort(red) and Frogsort2 (green); ‘0’ marks serial implementations, ‘1’,‘2’,‘4’,‘8’ mark the number of threads in threaded implementations; dashed lines show medians of all six groups.
Deep dive: deconstructing Timsort
Simple is better than complex … If the implementation is hard to explain, it’s a bad idea. — Tim Peters
Some languages and systems use Timsort behind their core sorting API (Python, Java, Android and Rust). Tim Peters - the author of Timsort is a clever and nice guy, and his algorithm is a masterpiece of algorithm engineering. After we have said these pleasantries, it is time to say clearly what Timsort is: rather an algorithm good at avoiding work on pre-sorted data than good at sorting non-sorted data. We believe that the main use-case of a sorting API is converting non-sorted data into sorted data, and not minimizing the work in case the data is already sorted. If data is already sorted, there are better ways - metadata - to avoid sorting it again. The usual justification for Timsort as the core algorithm behind a sorting API is the expectation that “More often than not, data will have some preexisting internal structure”. In the following we will deconstruct this argument, explain the problems of Timsort and show that it rarely is better than other algorithms.
These are the problems of Timsort
A good technical writer, trying not to be obvious about it, but says everything twice: formally and informally. Or maybe three times. — Donald Knuth
- Timsort is based on Natural-Mergesort, which is biased towards good performance on presorted data and rather not so good performance on non-sorted data
- the merge strategy of Timsort avoids movements on presorted data, but duplicates movements when it truly comes to merging
- Timsort heavily invests overhead and comparisons in the hope to save forthcoming comparisons and movements, for truly non-sorted data these investments are misinvested costs6
- while Timsort shows impressive speedups in presorted data (up to factor 20 faster than Mergesort), is is usually overlooked that Mergesort even without adaptivity-tuning is very adaptive to presorting (say factor 6), and hence Timsort realizes only small absolute savings on presorted data but big absolute losses when it comes to sorting tasks)
- Timsort shines if data is locally presorted and globally doesn’t need merging, on real real-world data Timsort is slow
- Timsort is so complicated, that an algorithmic bug escaped attention for 13 years7 and the attempt to fix it in Java resulted in yet another bug discovered 3 years later8
- implementing Timsort is rather tricky and it is inherently serial
Timsort is king in presorted data, but when sorting algorithms are needed for sorting APIs in a multicore-global-warming-world, then the greeNsort® algorithms are faster, more sustainable and can be parallelized. Furthermore the tuned greeNsort® algorithms eat deep into Timsorts domain and sometimes beat Timsort in adaptivity, as the following sections show.
There are better algorithms for real-world data than Timsort
If the standard is lousy, then develop another standard — Edward Tufte
While assuming some “preexisting internal structure” is reasonable, for a certain percentage of API-calls, Timsort wants extreme structure: Timsort can beat Mergesort and other algorithms if data is locally perfectly presorted and has strong global structure, such that few runs actually need merging and mostly just can be copied together. This is not what real-world data looks like, and if so, it does not need sorting. We choose to evaluate algorithms with a mix of four data generators that provide a realistic degree of structure:
- asclocal: \(\sqrt{N}\) locally sorted but overlapping
sequences of length \(\sqrt{N}\) need
global merging (the first half of the work is already done, the second
not)
- ascglobal: \(\sqrt{N}\) globally ascending blocks each with \(\sqrt{N}\)randomly permuted keys need local sorting (the first half of the work is sorting each block, the second part - global merging - can be skipped)
- tieboot: a bootstrap sample of \(1..N\) keys, this implies about \(2/3\) unique keys and \(1/3\) ties
- tiesqrt: \(N\) keys are sampled from only \(\sqrt{N}\) distinct keys, hence we have about \(\sqrt{N}\) tied values of each
The first two of these generators give fair opportunity to Timsort for exploiting preexisting internal structure. The second two generators provide week and strong opportunity to partitioning sorts such as Quicksort for exploiting ties. We expected Timsort to benefit from this structured portfolio, but Timsort not even convinces on the two semi-presorted use-cases. To our surprise Timsort was not faster than Knuthsort on the half-presorted data structures:
Timsort and competitors on four real-world data structures relative to Mergesort on the difficult tieboot input. The letters represent medians of 50 replications of \(N=2^{20}\) for each combination of input and algorithm: Timsort, Knuthsort, Frogsort1, Squidsort1, frogsort2, squidsort2. The KPIs are total memory (size), runtime (secs) and footprint (sizesecs).
This is because all compared algorithms are faster on the easier tiesqrt, asclocal and ascglobal inputs than on the more difficult tieboot inputs. All competitors are faster than Timsort, even on the two half-presorted data structures asclocal and ascglobal. The greeNsort® algorithms are also more sustainable, the ratios relative to Timsort can be read from the following chart:
greeNsort® algorithms relative to Timsort on four real-world data structures. The letters represent medians of 50 replications of \(N=2^{20}\) for each combination of input and algorithm: Timsort, Frogsort1, Squidsort1, frogsort2, squidsort2. The KPIs are total memory (size), runtime (secs) and footprint (sizesecs).
There are better adaptive algorithms than Timsort
Some circumstantial evidence is very strong, as when you find a trout in the milk — Henry David Thoreau
The following experiments shows how easily Timsorts performance breaks
down if the input data is not perfectly presorted. We take perfectly
ascending data, and disturb it with increasing amount of uniform random
data defined by a parameter \(e\). We
perform 20 experiments for \(e \in \{ 0,
1,\ldots, 19\}\) each replicated \(10
\cdot (20 - e)\) times, i.e. the easier experiments with shorter
runtimes are replicated more often. The input data is generated by the
R-function
seq(n-2^e, 0, length=n) + runif(n, 0, 2*(2^e-1)) and
visualized in the following chart:
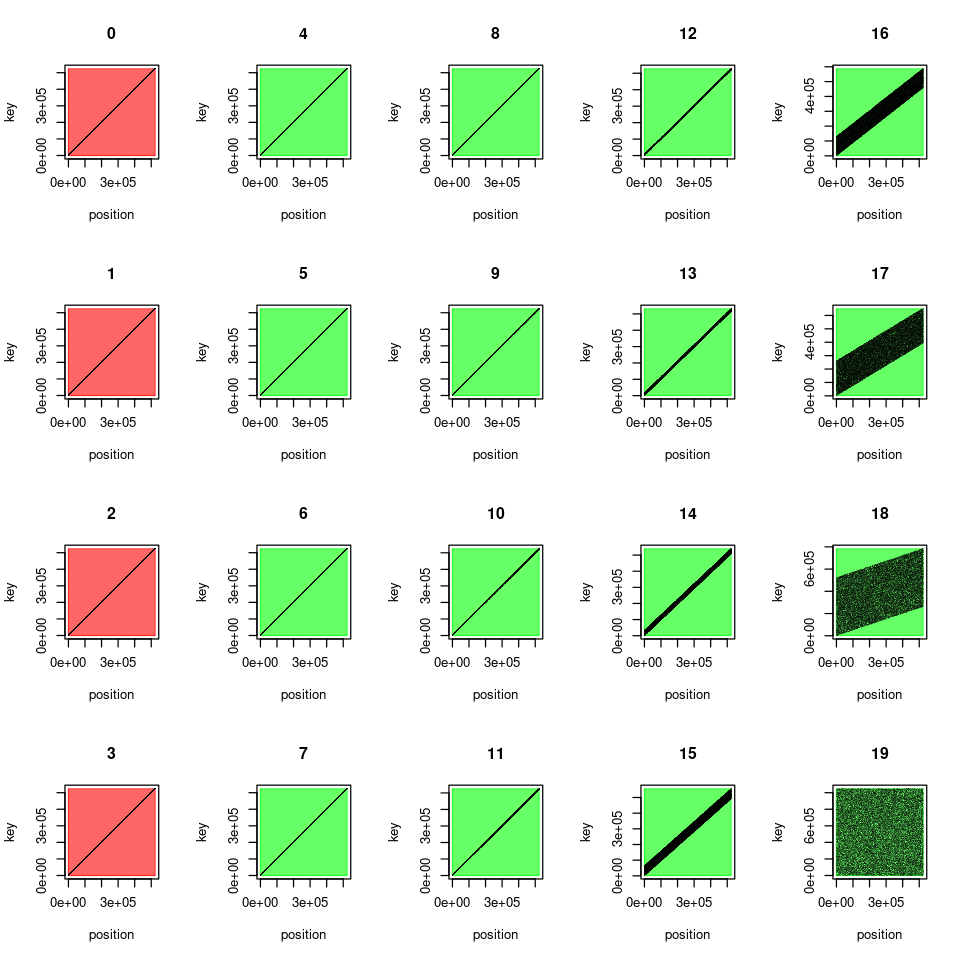
Ascending input data disturbed with uniform noise as a function of \(e \in {0,1,\ldots, 19}\). Background color red shows inputs for which Timsort is faster, green shows inputs for which classical Mergesort (and greeNsort® algorithms) are faster
Note that only in the few red experiments \(e \in {0,1,2,3}\) with very little random noise Timsort is faster than classical Mergesort. greeNsort® algorithms also beat Timsort for \(e = 3\) and some even for \(e=2\). The following charts give details and speak for themselves: their bars visualize the absolute losses and gains of greeNsort® algorithms over Timsort.
In most experiments Octosort is faster than Timsort, where not, only a little bit; Mergesort is also shown.
Frogsort1 is mostly faster than Timsort, and Squidsort1 tuned for adaptivity eats deep into Timsorts domain
Unlike Mergesort, Frogsort1 has also mostly lower footprint than Timsort, and Squidsort1 tuned for adaptivity eats deep into Timsorts domain
Tuned for memory and adaptivity, squidsort2 is faster than Timsort across the board, frogsort2 is a bit faster and less adaptive, Mergesort cannot compete with the greeNsort® algorithms.
Tuned for memory and adaptivity, squidsort2 has lower footprint than Timsort across the board, frogsort2 is a bit more sustainable but less adaptive and Mergesort cannot compete.
Even the low-memory walksort is almost as fast as Mergesort and faster than Timsort, grailsort cannot compete.
Timsorts performance breaks down even more if the input data is reverse-sorted. We repeat the above experiments with descending data disturbed by an increasing amount of noise. Let the charts speak for themselves:
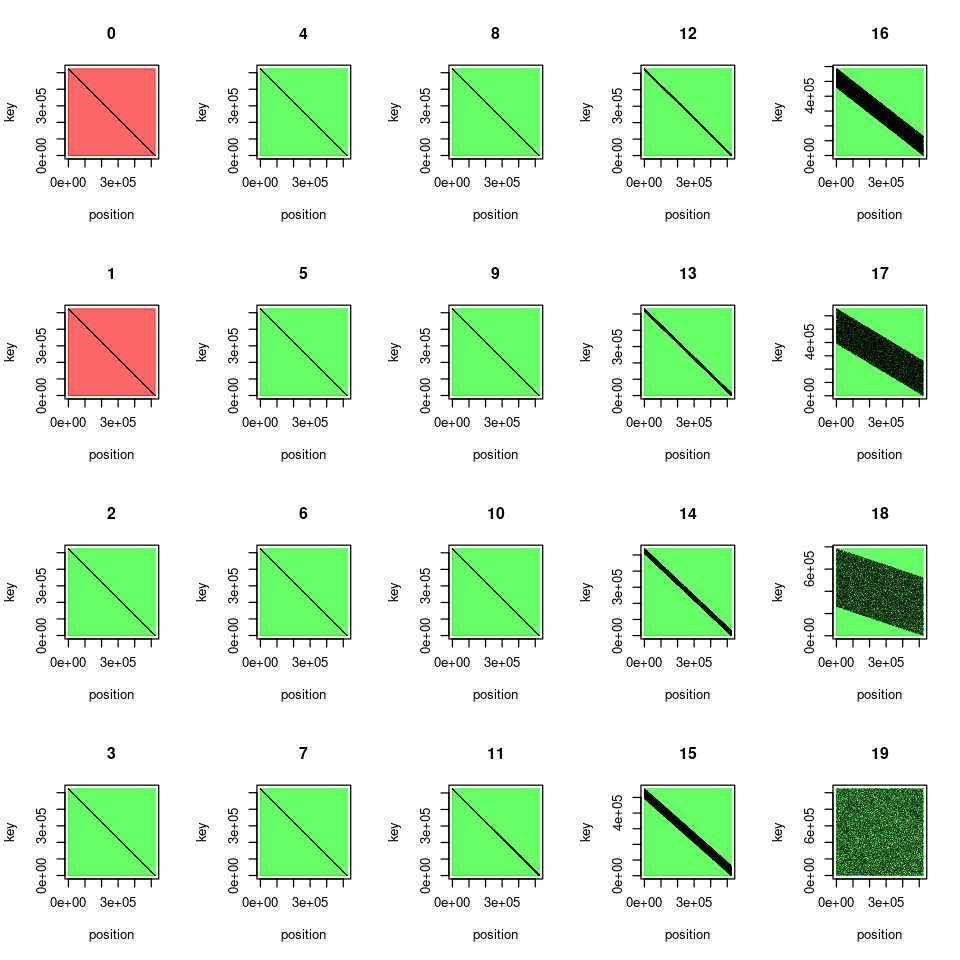
Only for un-disturbed and minimally disturbed data (red) is Timsort faster than Mergesort (and the greeNsort® algorithms)
Although Timsort has lower footprint than Mergesort, Octosort partially beats Timsort in its own domain
Except for perfectly reverse-sorted data, Frogsort1 is faster than Timsort, and even that is taken away by Squidsort1
Except for perfectly or minimally disturbed reverse-sorted data, Frogsort1 has lower footprint than Timsort, and even that is taken away by [Squidsort1]
Tuned for memory and adaptivity, the speed of squidsort2 blows Timsort out of the water, frogsort2 is a bit faster and less adaptive, and Mergesort cannot compete with the greeNsort® algorithms.
Tuned for memory and adaptivity, the footprint of squidsort2 blows Timsort out of the water, frogsort2 is a bit more sustainable but less adaptive, and Mergesort cannot compete.
Even the low-memory walksort is almost as fast as Mergesort and faster than Timsort, grailsort cannot compete.
A new, splitted API for Timsort?
I still have to lecture him [Guido van Rossum] about his true vision of what Python should be — Tim Peters
Now what is the true vision of what Timsort should be? Given that is cannot compete with many other sorting algorithms. Let’s rehearse where Timsort beats them all: if the data is locally presorted and globally needs just re-arrangement (copying, not merging) of identified quite non-overlapping runs. The implementation note of Javas stable sorting API says about Timsort: “It is well-suited to merging two or more sorted arrays: simply concatenate the arrays and sort the resulting array”. This is a call to waste energy, why should we ask Timsort to identify existing runs if we know them beforehand? Lets take the simple example of two sorted arrays and compare the costs:
| Proper way | Timsort way | |
|---|---|---|
| non-overlapping sequences | N allocations and N copies for concatenation | N allocations and N copies for concatenation, N comparisons for identifying runs, if not copied in the right sequence: another 0.5 N allocations and 1.5 copies |
| overlapping sequences | N allocations, N comparisons and N copies for merging | N allocations and N copies for concatenation, N comparisons for identifying runs, another 0.5 allocations and N comparisons and 1.5 N copies for merging |
So even in Timsorts domain of dealing with presorted non-overlapping sequences the Java suggestion is nonsensical. It would make more sense to split the serial Timsort into two easily parallelizable APIs
- a first API that identifies multiple runs of possibly varying lengths
- a second API that takes identified runs of possibly varying lengths, generates a merge-plan and executes it
However, in certain input patterns Timsorts restriction to only merge neighbor runs will turn out to be suboptimal and other strategies will be superior. But if the first API is not used in the Java example and the second API is heavily modified to merge non-neighbor runs, what is left for Timsort? Well, the “proper way of merging” fails, if the input sequences unexpectedly turn out not to be completely sorted! The “Timsort way” is robust against input problems. But again: then we should rather verify each input sequence with Timsort, and then call the second API which executes an optimal plan.
Finally we have peeled Timsort to its core: it is a robust \(\mathcal{O}(N)\) sorting verifier, most likely the best one possible, because it gracefully degrades to \(\mathcal{O}(N\log{N})\) sorting: Tim peters did a great Job on this. But when sorting algorithms are needed for sorting APIs in a multicore-global-warming-world, then the greeNsort® algorithms are faster, more sustainable and can be parallelized.
Results! Why, man, I have gotten a lot of results. I know several thousand things that won’t work. — Thomas Edison
All those algorithms have been fairly compared by us with similar implementation quality. Orson Peters (2015) Pattern Defeating Quicksort - see Pdqsort - is not on the above list, because his extremely professional and tuned C++ implementation cannot be compared. Theoretically the greeNsort® algorithms are slightly more efficient however, this has yet to be empirically checked↩︎
Exceptions are Tim Peters Timsort the implementation of Timothy Van Slyke is used, and Huang&Langston’s Grailsort and related algorithms implemented by Andrey Astrelin↩︎
Note that Timsort is lower than proper standard textbook Mergesort on all four input data patterns, including globally presorted data and locally presorted data↩︎
Note that Sqrtsort can only sort equally sized elements, whereas Frogsort2 can handle elements of different size↩︎
“Developing Green Software”, no longer available at software.intel.com/content/dam/develop/external/us/en/documents/developing-green-software-183291.pdf↩︎
The implementers of Timsort in Rust have realized that and implemented Timsort without ‘galopping mode’.↩︎
Gow et. al. (2015) “OpenJDK’s Java.utils.Collection.sort() Is Broken: The Good, the Bad and the Worst Case”↩︎
Auger et. al. (2018) “On the Worst-Case Complexity of TimSort”↩︎
Copyright © 2010 - 2024 Dr. Jens Oehlschlägel - All rights reserved - Terms - Privacy - Impressum
